Page 150 - 201901

146 2019 年 1 月

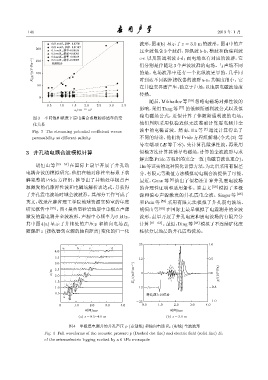
波形，图4(b) 显示了z = 3.0 m的波形。图4中的声
0.02 mol/L, பဋ=0.07501
0.05 mol/L, பဋ=0.01387
200
0.1 mol/L, பဋ=0.00636 压全波包含 3 个波群，即纵波 b-b、横波和伪瑞利波
0.2 mol/L, பဋ=0.00303
0.4 mol/L, பဋ=0.00109 c-c 以及斯通利波 d-d；而电场也有对应的波群，它
Κ SP /(nVSPa -1 ) 100 ጳভલՌ 们分别是伴随这 3 个声波波群的电场。与声场不同
0.6 mol/L, பဋ=0.00009
150
的是，电场波形中还有一个比纵波更早的、几乎同
50 时到达不同源距接收器的波群a-a，其幅度很小。它
在井壁交界面产生，独立于声场，以地层电磁波速度
传播。
0
随后，Mikhailov 等 [56] 忽略电磁场对弹性波的
0.5 1.0 1.5 2.0 2.5 3.0 3.5 [57]
κ/10 -12 m 2 影响，采用 Tang 等 的低频斯通利波公式以及似
稳电磁场公式，近似计算了伴随斯通利波的电场。
图 3 不同饱和浓度下震电耦合系数随渗透率的变
化关系 他们判断采用似稳近似无法准确计算震电测井全
Fig. 3 The streaming potential coefficient versus 波中的电磁首波。然而，Hu 等 [7] 通过计算得出了
permeability at different salinity 不同的结论，他们将 Pride 方程组解耦 (令式 (2) 等
号右端项 LE 等于零)，先计算孔隙弹性波，再采用

3 井孔动电耦合波模拟计算 似稳方法计算其诱导电磁场，计算的全波波形与求
解完整Pride方程组的完全一致 (电磁首波也重合)。
胡恒山等 [53−54] 在国际上最早开展了井孔动 Hu等证实的这种简化计算方法，为之后采用有限差
电耦合波的模拟研究，他们在轴对称柱坐标系下求 分、有限元等数值方法模拟动电耦合波提供了可能。
解完整的 Pride 方程组，推导出了井轴处单极点声 最近，Guan 等 [8] 给出了似稳法计算井孔震电波场
源激发的孔隙弹性波和电磁场解析表达式，并获得 的合理性证明和适用条件。崔志文 [58] 模拟了多极
了井孔震电波场时域全波波形。其部分工作写成了 源和偏心声源激发的井孔震电全波。Singer 等 [45]
英文，收录在麻省理工学院地球资源实验室的年度 和 Pain 等 [59] 采用有限元法模拟了井孔震电波场。
研究报告中 [55] 。图4是典型砂岩地层中单极点声源 胡恒山等 [60] 在国际上最早模拟了电震测井的全波
激发的震电测井全波波形，声源中心频率为 6 kHz。 波形，最早开展了井孔电震和震电波场的有限差分
计算 [61−63] 。最近，Ding等 [64] 模拟了不连续矿化度
其中图 4(a) 显示了井轴处的声压 p 和轴向电场 E z
随源距z (接收器到点源的轴向距离)变化的归一化 柱状分层地层的井孔震电波场。

25 1.0
a b c d
4.0
3.5 12 0.5
3.0
2.5
z/m 2.0 E z/(mVSm -1 ) 0 0.0 p/(10 5 Pa)

1.5
b c d
1.0 -12 0 -0.5
0.5 ࠲E z ஊܸφՑ
a
-25 -1.0
0 1.0 2.0 3.0 4.0 0.0 1.0 2.0 3.0 4.0
௑ᫎ/ms ௑ᫎ/ms
(a) z=0.5~4.0 m (b) z=3.0 m

图 4 单极震电测井的井孔声压 p (点划线) 和轴向电场 E z (实线) 全波波形
Fig. 4 Full waveforms of the acoustic pressure p (Dashed dot line) and electric field (solid line) E z
of the seismoelectric logging excited by a 6 kHz monopole