Page 130 - 201806

960 2018 年 11 月

回归诊断分为回归诊断与异常点诊断。本次仿 变量采用变量筛选法进行处理并起到降维功能。
真以条件指数 k (无量纲) 与方差膨胀因子 vif (无 在进行降维的过程中，主要是通过多元回归原
量纲) 为回归诊断指标，应用统计软件 SAS 完成指 理建立回归方程，先找出输入变量集的主分量，然后
标计算 [22] 。 通过 F 统计量计算各变量的显著性水平，最终决定
最终计算出k 和vif 的值如表2所示。 出删除的输入变量，确定出主分量回归方程，实现
当 1 6 k 6 10 时，变量间为无共线性关系；当 降维。
10 < k 6 30 时，变量间有中等共线性关系；当
表 3 异常点诊断结果
k > 30 时，变量间有严重共线性关系。当 vif > 10
时，变量间有严重共线性关系。由计算值可进行判 Table 3 Some diagnosis of outlier
别，本次仿真输入变量间存在严重共线性影响。
样本点 学生化残差 COOKD
对样本进行学生化残差以及 COOKD 值计算，
331 2.345 0.003
确定出异常点，并将其剔除出样本实验库，提高预测 332 2.753 0.005
精度。异常点诊断结果如表3所示。 333 2.555 0.006
因已判断出输入变量间存在严重共线性影响， 364 −2.102 0.007
为提高预测速率和准确度，本次实验对共线性的 390 −2.203 0.004
402 2.068 0.005
表 2 条件指数 k 与方差膨胀因子 vif 419 −2.485 0.008
Table 2 Condition indices and variance 461 −2.903 0.005
inflation factors 465 −2.108 0.006
变量 vif k
3.3 改进的GA-SVR预测仿真
1.60384 1.03120
X 1
经分析研究发现基于 SVR 进行风电机组噪声
X 2 3.54732 2.16532
预测模型的建立时，采用高斯核函数更适应于噪
X 3 12177659 198730
X 4 495630 4.01231 声特性。而 GA 能够快速有效地对模型参数进行寻
X 5 1.46302 469889 优，并得到很好的寻优结果。首先仅用改进后的
X 6 583721 7.50321 GA-SVR 对风电机组噪声信号进行预测仿真，预测
39911730 2910532
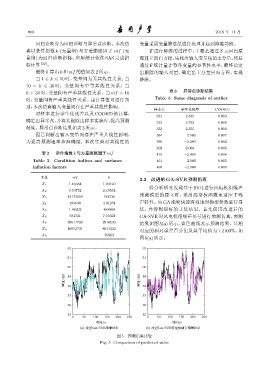
X 7 结果如图 5(a) 所示，蓝色曲线表示预测结果。其相
40353721 8611223
对应的相对误差百分比及其平均值为 1.2103%，如
X 8
X 9 70563
图6(a)所示。
62 62

61 61

60 60
ܦԍ/dB 59 ܦԍ/dB 59

58
58
57 57
56 56

55 55
0 50 100 150 200 250 0 50 100 150 200 250
௑ᫎ/s ௑ᫎ/s
(a) ஈᤉGA-SVRᮕ฾ፇ౧ (b) ஈᤉGA-SVRྲढ़ጟᚸՌᮕ฾ፇ౧
图 5 预测结果比较
Fig. 5 Comparison of predicted value