Page 60 - 应用声学2019年第4期

520 2019 年 7 月

最终，软输入 WRLS(SWRLS) 信道估计算法 是说，采用 SWRLS 进行信道估计的迭代接收机性
总结如下 [27−28] ： 能明显优于基于 HRLS 的迭代接收机，性能差距在
ˆ H ¯
b
e n = r n − h n−1 n , (23) 1.1 dB左右。
{ 0
( 2 2 2 ) 10
ˆ q n = tr diag σ (n) , σ (n−1) , · · · , σ (n−L+1)
b
b
b
10 -1
}
( ) 2
ˆ H
ˆ
× h n−1 h n−1 + P n−1 + σ , (24)
η
10 -2
¯
P n−1 b n
k n = , (25) BER 10 -3
¯
¯H
λˆq n + b P n−1 b n
n
ˆ
ˆ
∗
h n = h n−1 + k n e , (26) 10 -4
n
1 ( ¯ H ) 10 -5
P n = I − k n b n P n−1 . (27)
λ
10 -6
4 5 6 7 8 9 10 11 12
2 仿真分析 උྲ٪ܦඋ/dB
ࣃᅼη᥋ SWRLSͥᝠη᥋
ᤖ̽0൓ ᤖ̽2൓ ᤖ̽0൓ ᤖ̽2൓
本 节 主 要 是 在 时 不 变 频 率 选 择 性 衰 落 信 ᤖ̽1൓ ᤖ̽4൓ ᤖ̽1൓ ᤖ̽4൓
道 条 件 下 仿 真 算 法 性 能， 时 不 变 信 道 为 h = (a) SWRLS֗ࣃᅼη᥋ভᑟࠫඋ
T
(−0.691 − 0.501i, 0.361 + 0.506i, −0.528 − 0.408i) ， 10 0
其信道幅频特性曲线如图 3 所示。由图可知该信道 10 -1
存在一个 42 dB 的深衰点；由于性能的需求，本文
10 -2
仿真与试验数据处理中均采用软判决驱动的迭代
DFE。 BER 10 -3
10 10 -4
5
0 10 -5
ॆʷӑᛰᗀࣨए/dB -10 4 ᤖ̽0൓ 6 උྲ٪ܦඋ/dB 9 ᤖ̽0൓ 10 11 12
-5
-6
10
8
7
5
-15
-20
ࣃᅼη᥋
HRLSͥᝠη᥋
-25
ᤖ̽2൓
ᤖ̽2൓
-30
-35 ᤖ̽1൓ ᤖ̽4൓ ᤖ̽1൓ ᤖ̽4൓
(b) HRLS֗ࣃᅼη᥋ভᑟࠫඋ
-40
10 0
-45
0 0.5 1.0
ॆʷӑᮠဋ 10 -1
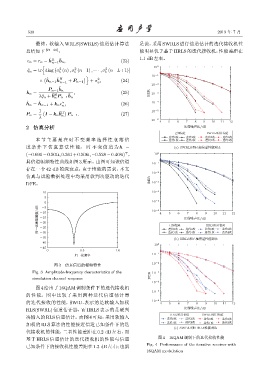
图 3 仿真信道的幅频特性 10 -2
Fig. 3 Amplitude-frequency characteristics of the 10 -3
simulation channel response BER
10 -4
图 4 给出了 16QAM 调制条件下的迭代接收机
10 -5
的性能。图中比较了采用两种迭代信道估计器
的迭代接收的性能，SWRL 表示的是软输入加权 10 -6 4 5 6 7 8 9 10 11 12
RLS(SWRL) 信道估计器，而 HRLS 表示的是硬判 උྲ٪ܦඋ/dB
HRLSͥᝠη᥋ SWRLSͥᝠη᥋
决输入的 RLS 信道估计。由图 4 可知：采用软输入 ᤖ̽0൓ ᤖ̽2൓ ᤖ̽0൓ ᤖ̽2൓
加权的 RLS 算法的性能接近信道已知条件下的迭 ᤖ̽1൓ ᤖ̽4൓ ᤖ̽1൓ ᤖ̽4൓
(c) SWRLS֗HRLSভᑟࠫඋ
代接收机的性能，二者性能差距在 0.2 dB 左右，而
基于 HRLS 信道估计的迭代接收机的性能与信道 图 4 16QAM 调制下的迭代接收性能
已知条件下的接收机性能差距在 1.3 dB 左右；也就 Fig. 4 Performance of the iterative receiver with
16QAM modulation