Page 54 - 《应用声学》2020年第2期

212 2020 年 3 月

T 同时，对于每一个松弛变量，支付一个代价 C，
距离超平面最近的这几个样本点满足y i (W x i
+b)=1，它们被称为“支持向量”。虚线称为边界，两 目标函数变为
条虚线间的距离称为间隔，用γ 表示： m
1 2 ∑
||W || + C ζ i , (9)
γ = 2/||W ||. (5) 2
i=1
通过求取 ||W || 的最小值，可以得到最优分类超 其中，C > 0 为惩罚参数，C 值大时对误分类的惩罚
平面。 增大，C 值小时对误分类的惩罚减小。要使式 (9) 取

最小值，则需要间隔尽量大，同时使误分类点的个数
x 
Wx֓b/ 2/||W|| 尽量少，C 是调和两者的系数。然后，就可以采用与
Wx֓b/
线性可分SVM一样的方法进行学习。

W Wx֓b/֓ 3.2 次声事件识别
通过对采集的次声数据进行分析，从中提取出
507 个噪声数据，加入采集的 108 个事件数据，进行

基于 SVM的次声事件识别实验。实验中，分别从噪
声数据和事件数据中随机抽取 4/5的样本作为训练
x 
集，对SVM进行训练，其余样本作为测试集，以检验
b/||W||
训练得到的 SVM 的分类能力。为了消除训练集和
图 6 SVM 的原理示意图
Fig. 6 Diagrammatic sketch of SVM 测试集随机选取带来的影响，实验进行多次运行，然
3.1.2 核函数 后对结果进行统计。
当进行两层小波包分解时，得到 4 个频带的能
对于非线性问题，上述方法并不能有效解决。
量 (E 1 、E 2 、E 3 、E 4 )，由于高频段的 E 3 和 E 4 趋于 0，
这种情况下，SVM采用的方法是将训练样本从原始
空间映射到一个更高维的空间，使得样本在这个空 所以选取特征向量 V = (E 1 /E, E 2 /E)，特征向量
间中线性可分，如果原始空间维数是有限的，即属性 的维数等于 2，此时分类效果比较差，在最好的情况
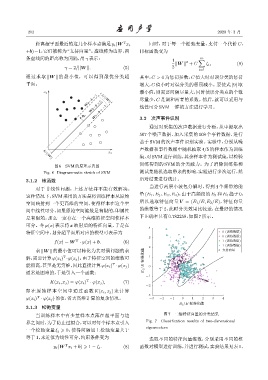
是有限的，那么一定存在一个高维特征空间使样本 下正确率只有0.782258，如图7所示。
可分。令 φ(x) 表示将 x 映射后的特征向量，于是在
4
特征空间中，划分超平面所对应的模型可表示为 0 (䇝㓳ᮠᦞ)
3 0 (䇝㓳ᮠᦞ)
f(x) = W T · φ(x) + b. (6) 1 (䇝㓳ᮠᦞ)
1 (䇝㓳ᮠᦞ)
2
求||W || 的最小值可以转化为其对偶问题的求 ᭟ᤱੁ䟿
T
解，需要计算φ(x i ) ·φ(x j )。由于特征空间的维数可 E ⊳E ಖюӑϙ 1
T
能很高，甚至是无穷维，因此直接计算φ(x i ) ·φ(x j ) 0
通常是困难的，于是引入一个函数：
-1
T
K(x i , x j ) = φ(x i ) · φ(x j ), (7)
-2
即在原始样本空间中通过函数 K(x i , x j ) 来计算
-3
T
φ(x i ) · φ(x j )的值，省去高维计算的复杂情况。 -3 -2 -1 0 1 2 3 4
E ⊳E ಖюӑϙ
3.1.3 松弛变量
当训练样本中有少量样本点落在超平面与边 图 7 二维特征向量的分类结果
界之间时，为了防止过拟合，可以对每个样本点引入 Fig. 7 Classification results of two-dimensional
eigenvectors
一个松弛变量 ξ i > 0，使得间隔加上松弛变量大于
等于1，来近似为线性可分，约束条件变为 选取不同的特征向量维数，分别采用不同的核
T
y i (W x i + b) > 1 − ζ i . (8) 函数对模型进行训练，并进行测试，实验结果见表1。