Page 53 - 《应用声学》2020年第2期

第 39 卷 第 2 期 吴涢晖等： 应用支持向量机和人工神经网络对大气次声信号识别的初步实验 211

5
0
-5
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(a) ㅜ3ቲ0㢲⛩䟽ᶴؑਧ
10
0
-10
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(b) ㅜ3ቲ1㢲⛩䟽ᶴؑਧ
0.1
0
-0.1
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(c) ㅜ3ቲ2㢲⛩䟽ᶴؑਧ
1
0
-1
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(d) ㅜ3ቲ3㢲⛩䟽ᶴؑਧ
0.005
0
-0.05
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(e) ㅜ3ቲ4㢲⛩䟽ᶴؑਧ
0.01
0
-0.01
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(f) ㅜ3ቲ5㢲⛩䟽ᶴؑਧ
0.05
0
-0.05
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(g) ㅜ3ቲ6㢲⛩䟽ᶴؑਧ
0.05
0
-0.05
0 200 400 600 800 1000 1200 1400 1600 1800 2000
(h) ㅜ3ቲ7㢲⛩䟽ᶴؑਧ
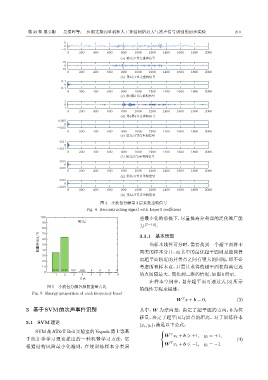
图 4 小波包分解第 3 层系数重构信号
Fig. 4 Reconstructing signal with Layer3 coefficient

100 差最小化的前提下，尽量提高分类器的泛化推广能
90 ኄ3ࡏ
力 [7−10] 。
80
ᑟ᧚ᄈѬඋ/% 60 3.1.1 基本思想
70
当样本线性可分时，需要找到一个超平面将不
50
40
30 同类的样本分开，而其中的最优超平面则是能使得
离超平面较近的异类点之间有更大的间隔，即不必
20
10 考虑所有样本点，只需让求得的超平面使得离它近
35.76 63.55 0.01 0.69 0 0 0 0
0
1 2 3 4 5 6 7 8 的点间隔最大。简化到二维的情况，如图6所示。
ᓬག
在样本空间中，划分超平面可通过式 (3) 所示
图 5 小波包分解各频段能量占比
的线性方程来描述：
Fig. 5 Energy proportion of each frequency band
T
W x + b = 0, (3)
3 基于SVM的次声事件识别 其中，W 为法向量，决定了超平面的方向；b 为位
移量，决定了超平面与原点的距离。对于训练样本
3.1 SVM理论
(x i , y i )，满足以下公式：
SVM是AT&T Bell实验室的Vapnik博士等基 
T
 W x i + b > +1, y i = +1,
于统计学学习理论提出的一种机器学习方法，它 (4)
T
 W x i + b 6 −1, y i = −1.
根据结构风险最小化准则，在使训练样本分类误