Page 109 - 《应用声学》2020年第4期

第 39 卷 第 4 期 倪辉等： 10 kV 交联聚乙烯电缆中超声波传播规律 595

能量分散的现象。每个检测点测得 3 组数据，滤 峰 -峰值衰减速度最快，此规律和仿真一致，从而也
除噪声后求得峰峰值的平均值 U p-p ，将 U p-p 和传播 证明了前文超声波在电缆中扩散过程理论的正确
距离 x 进行曲线拟合，最佳拟合公式如式 (3) 所示， 性。因此，针对实验中规格的电缆局放超声检测，
2
拟合曲线如图 12 所示，可决系数 R = 0.96，可见， 传感器布置在距局放易发位置 100 mm 以内比较
实际电缆中超声波幅值随传播距离的衰减是符合 合理。
指数规律的，此规律可以用于电缆局放位置或局 如图 9 所示，若将 L 3 = 100 mm 处确定为扩散
放强度的估算。其衰减系数.α = 0.07 Np/mm (或 过程结束位置，此时波阵面平面化程度用扩散半径
0.62 dB/mm)，U 0 = 1678.63 mV，已知超声波在硅 r 和电缆直径2R 0 之比k 表示：
√
橡胶材料中衰减系数为 0.40 dB/mm [22] ，实际电缆 2 2
L + (2R 0 − R 1 )
3
结构中超声波衰减系数是其 1.55 倍，所以实际电缆 k = = 2.42. (4)
2R 0
结构中超声波的衰减相对来说是比较严重的，其原
k 值越大，波阵面相对越接近平面。本文中电缆k 值
因和电缆本身结构复杂有关，比如电缆的钢铠层和
大于 2.42 就可以判定波阵面已经近似平面，扩散过
外护套及内护套之间实际上有很多气隙，会加剧超
程基本结束。因此可以按照公式 (4) 的原理来估计
声波的衰减，这无疑增加了电缆局放超声波检测的
任意型号电缆中声波扩散过程结束的位置。
难度，对传感器的灵敏度提出了更高的要求。
U p-p = U 0 e −α·x . (3) 4 讨论

并且，从图 12 显然可以发现，在约 100 mm 将图 7 所示声压图的颜色图例范围调小至
7
处是一个转折点，从声源至 100 mm 之间超声波 10 Pa 得到如图 13 所示的声压分布图。对比图 7
和图 13 可发现，电缆中的声波可以分为两个分量：
200
20 mm 一个分量声波幅值较大 (主要分量)，如图 7 所示，约
0
在10 Pa的数量级，其在整个电缆结构中的传播速
9
-200
0 0.2 60 mm 0.4 度基本一致；另一个分量声波幅值较小 (次要分量)，
10
U/mV 0 如图13所示，约在10 Pa的数量级，其在铜芯中的
7
-10
0 0.2 0.4 t=20 µs
4 100 mm
0
-4
0 0.2 0.4
t/ms
t=40 µs
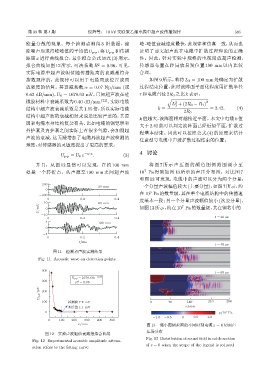
图 11 检测点声波实测结果
Fig. 11 Acoustic wave on detection points

400
t=60 µs
U p-p =1678.63e -0.07
300
2
R =0.96
U p-p /mV 200

100 ೝ฾ϙ 7.2 mV 0 70 140 210 280
લՌϙ 1.1 mV x/mm
0 p/10 Pa
7
-1.0 -0.5 0 0.5 1.0
0 100 200 300 400 500
x/mm 图 13 缩小图例范围的不同时刻电缆 z = 0 切面声
压场分布
图 12 实验声波幅值衰减指拟合曲线
Fig. 13 Distribution of sound field in cable section
Fig. 12 Experimental acoustic amplitude attenu-
of z = 0 when the scope of the legend is reduced
ation refers to the fitting curve