Page 104 - 《应用声学》2021年第2期

272 2021 年 3 月

的时间位移为 τ，顺流或逆流下的时间差测量方式 中将计算得到的传播时间定义为对比值，实验得到
相同，分别设为t s 、t n ，则 的传播时间为测量值，测量结果如表 1 所示。由表 1
可知，误差较为稳定且普遍小于 0.8%；首次测量时，
t s (t n ) = t z + τ − t 0 − t correction , (9)
系统参考波形参数设置没有基于实际情况，会选用
其中，t correction 为修正时间，包括管壁误差、电路延 某一波形作为参照波形，这也导致首次互相关计算
迟以及流体流态等造成的影响时间 [8] 。 时比之后的值误差较大，因此在表 1 中第一个测量

值的误差会达到0.73%。
3
̉ᄱТᝠካ
2

1
ࣨϙ/V 0
τ
-1
͜୧௑ᫎ
-2
t  t z
-3
图 5 时间差自补偿原理图 0 1 2 3 4 5
௑ᫎ/ms
Fig. 5 Schematic diagram of time difference self-
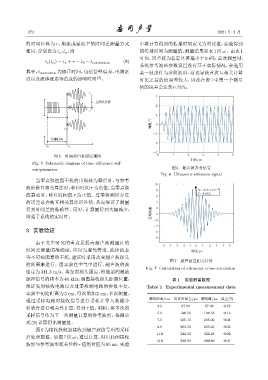
compensation 图 6 超声波参考信号
Fig. 6 Ultrasonic reference signal
当零点取值因干扰的出现较为靠后时，与参考
10
波形做互相关算法时，移位时间τ 为负值；当零点取
8 X.֓⊲T -8
值靠前时，移位时间值 τ 为正值。过零检测所存在 6 Y . ⊲
的误差总会被互相关算法所补偿，从而保证了测量 4
得到时间差的准确性。同时，计算量得到大幅减少， 2
增强了系统的实时性。 ̉ᄱТϙ 0
-2
-4
3 实验验证 -6

-8
由于文中研究的重点是提高超声波测量计的
-5 -4 -3 -2 -1 0 1 2 3 4 5
时间差测量的准确度，所以为避免管道、流体流态 ௑ᫎ/ms
等不可控因素的干扰，验证时采用改变超声波探头
图 7 超声波互相关计算
的距离来进行。因实验在空气中进行，超声波的波
Fig. 7 Calculation of ultrasonic cross-correlation
速定为 341.3 m/s。将发射探头固定，换能器的激励
脉冲信号的频率为40 kHz，调整接收探头距离位置， 表 1 实验测量数据
保证发射接收电路以及过零检测电路的参数不变。 Table 1 Experimental measurement data
实验中初始距离为 3 cm，每次增加2 cm，多次测量。
通过采样电路对接收信号进行采样并导入数据分 测量距离/cm 对比时间差/µs 测量值/µs 误差/%
析软件进行相关性计算，得到 τ 值。同时，将本次的 3.0 87.90 87.26 0.73
5.0 146.50 146.33 0.12
采样信号作为下一次测量计算的参考波形。根据公
7.0 205.10 205.02 0.04
式(9)计算得出测量值。
9.0 263.70 263.65 0.02
图6 为接收换能器接收到超声波信号后的采样
11.0 322.30 322.24 0.02
后处理图像。如图 7 所示，通过计算，得出此例接收
13.0 380.90 380.86 0.01
波形与参考波形相关性的τ 值绝对值为85 ns。实验