Page 99 - 《应用声学》2021年第2期

第 40 卷 第 2 期 宋明鑫等： 声表面波器件变频快速模拟方法 267

谐振器的导纳计算结果。图中红色线为 HCT-FEM 利用本文快速计算方法，只需建立一个参考模型，该
基于参考单元计算得到的谐振器导纳幅值与实部； 模型对应着一个波长值，然后，利用式 (12) 可获得
黑色线是利用快速变频方法将波长为4.01 µm时的 任意波长的单元系统矩阵，该过程只涉及矩阵的简
计算结果。从图4中可知，参考模型的谐振频率与反 易乘法，避免了需要对每一波长值进行建模和相关
谐振频率为 987.7 MHz 与 1027.2 MHz。当波长调 处理过程，从而节省了大量的时间，模拟效率大大
整为4.01 µm时，导纳曲线的位置整体左移，谐振频 提升。
点与反谐振频点出现在 985.1 MHz 与 1024.6 MHz，
10 1
频移的大小为 2.6 MHz。两者谐振点处幅值的微小 ӭЋथവ
ঌᤴԫᮠவข
差异来自于电极阻抗的变化。 10 0

10 1 10 -1
λ=4.00 mm
λ=4.01 mm ࠮ጪ/W -1
10 0 10 -2
10 -1 10 -3
࠮ጪ/W -1 10 -2

10 -4
10 -3
0.96 0.98 1.00 1.02 1.04 1.06 1.08
9
10 -4 ᮠဋ/10 Hz
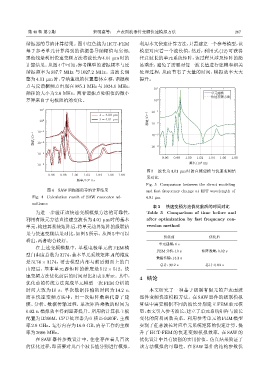
图 5 波长为 4.01 µm 时的直接建模与快速变频结
0.96 0.98 1.00 1.02 1.04 1.06 1.08
果对比
9
ᮠဋ/10 Hz
Fig. 5 Comparison between the direct modeling
图 4 SAW 谐振器的导纳计算结果 and fast frequency change at IDT wavelength of
Fig. 4 Calculation result of SAW resonator ad- 4.01 µm
mittance
表 3 快速变频方法优化前后的时间对比
为进一步验证该快速变频模拟方法的可靠性， Table 3 Comparison of time before and
利用有限元方法直接建立波长为 4.01 µm时的基本 after optimization by fast frequency con-
单元，构建其系统矩阵后，将单元边界矩阵的级联结 version method
果与快速变频结果对比，如图 5所示。从图 5中可以
优化前 优化后
看出，两者吻合较好。
单元建模：6 s
在上述变频模拟中，单根电极单元的 FEM 模
FEM 分析：10 s 矩阵数乘：0.02 s
型自由度总数为 3174，基本单元系统矩阵A 的维度
数据传输：14.2 s
是 3174 × 3174，消去模型内部与前后侧面上的自
总计：30.2 s 总计：0.02 s
由度后，基本单元 B 矩阵的维度是 512 × 512。快
速变频方法优化前后的时间对比如表3 所示。其中， 4 结论
优化前的传统方法完成单元模型一次 FEM 分析的
时间大致为 10 s，单次数据传输的时间为 14.2 s。 本文研究了一种基于级联有限元的声表面波
而在快速变频方法中，用一次矩阵数乘代替了建 器件变频快速模拟方法。在 SAW 器件的级联模拟
模、分析、数据传输过程，单次矩阵乘数的时间为 算法中需要根据不同的波长分别建立 FEM 单元模
0.02 s，模拟效率得到显著提升。所用的计算机主板 型，本文引入参考波长，建立了单元系统矩阵与波长
配置为 B360M，CPU 处理器为 6 核 i5-9400F，主频 变化的简易函数关系。利用参考单元的 FEM 模型
率2.9 GHz。运行内存为 16.0 GB，内存工作的主频 实现了任意波长对应单元系统矩阵的快速计算，提
率为2666 MHz。 升了 HCT-FEM 的快速变频模拟效率，在 SAW 的
在 SAW 器件参数设计中，往往存在着几百次 优化设计中具有较强的实用价值。仿真结果验证了
的优化过程，即需要对几百个波长值分别进行模拟。 该方法模拟的可靠性。在 SAW 器件的结构参数优