Page 20 - 《应用声学》2021年第5期

664 2021 年 9 月

该模型将系统接收到的超声回波信号 y(t) 表
示为试样不同界面和缺陷反射回波信号 s i (t) 的线
性组合，其中 s i (t)可以表示为反射系数c i 和入射信
号x i (t − t i )的乘积 [35−36] ，即
n
∑
y(t) = c i x i (t − t i ) + ξ(t). (6)
i=1
同样考虑对叠层封装裸片之间的界面进行超
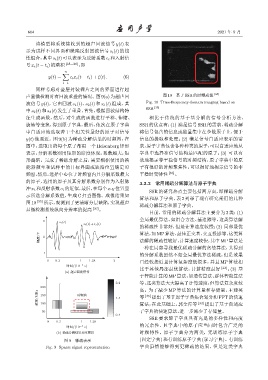
声显微检测时有回波重叠的情况。图9(a)为超声回 图 10 基于 SSR 的时频成像 [35]
波信号 y(t)，它由回波 s 1 (t)、s 2 (t) 和 s 3 (t) 组成，其 Fig. 10 Time-frequency domain imaging based on
中s 2 (t) 和s 3 (t) 发生了重叠，首先，根据回波结构特 SSR [35]
征生成函数，然后，对生成的函数进行平移、伸缩、 相比于传统的基于基分解的信号分析方法，
旋转等变换，得到原子字典，最后，依次在原子字典 SSR的优点有：(1) 满足信号 SSR的需求，稀疏分解
中自适应地选取若干个相关性最好的原子对信号 将信号包含的信息或能量集中在少数原子上，便于
y(t) 做逼近。图 9(b) 为稀疏分解结果的时频图，在 信息的提取和处理；(2) 满足信号自适应表示的需
图中，选取出的每个原子都用一个 Heisenberg 矩形 求，原子字典包含各种种类的原子，可以自适应地从
表示，分解系数则用矩形的暗度体现，系数越大，矩 字典中选择和信号结构最匹配的原子；(3) 可以有
形越暗。完成了稀疏分解之后，需要根据使用的换 效地揭示非平稳信号的时频结构，原子字典中的原
能器频率和试样中的目标界面或缺陷位置确定时 子有很好的时频聚焦性，可以很好地揭示信号的非
频窗，然后，选择中心位于时频窗内且分解系数最大 平稳时变特性 [33] 。
的原子，选用的原子及其分解系数分别作为入射脉
3.3.2 常用稀疏分解算法与原子字典
冲x i 和反射系数c i 的近似，最后，在每个x-y 位置显
SSR 的研究热点主要包括两方面，即稀疏分解
示所选分解系数值，生成 C 扫查图像。成像结果如
算法和原子字典，表 2 列举了现有研究采用的几种
图 10 [35] 所示，观测到了更清晰分层缺陷，实现超声
稀疏分解算法和原子字典。
显微检测系统纵向分辨率的提高 [36] 。
目前，常用的稀疏分解算法主要分为 3 类：(1)
全局最优算法，如组合方法、基追踪等，这类算法解
1 s ↼t↽
s ↼t↽⇁s ↼t↽
的稀疏性非常好，但是计算速度较慢；(2) 局部最优
ࣨए/V 0 算法，如MP算法、最佳正交基、交互投影等，这类算
法解的稀疏性较好，计算速度较快，其中MP算法是
一种在局部寻找最优稀疏分解的贪婪算法，其得到
-1
的分解系数虽然不如全局最优算法稀疏，但是效果
0 0.3 1 1.28 2
已经较接近且计算复杂度低很多，并且 MP 算法相
௑ᫎ/(10 -7 s)
比于其他局部最优算法，计算精度最好 [33] ；(3) 基
(a) ᡔܦڀฉηՂ
于智能计算的 MP算法，如遗传算法、群体智能算法
等，这类算法大大提高了计算速度，但算法复杂度较
2.4
ᮠဋ/MHz 200 ௑ᮠቔ 1.4 高。为了减少 MP 算法的计算量和存储量，王建英
150
等
提出了基于原子字典集合划分和FFT的快速
[45]
[33]
算法；在此基础上，郭金库等
提出了基于自适应
100
50 子字典的快速算法，进一步减少了存储量。
0.4
SSR 要求原子字典具有充足的多样性和高度
0 0.3 1 1.28
的冗余性，且字典中的原子应当同时包含广泛的
௑ᫎ/(10 -7 s)
(b) ሪႠѬᝍፇ౧ԣ௑ᮠቔ 时频特性，原子字典分为两类，无训练原子字典
图 9 稀疏表示 (固定字典) 和有训练原子字典 (学习字典)。有训练
Fig. 9 Sparse signal representation 字典虽然能够得到更稀疏的结果，但是这类字典