Page 114 - 《应用声学》2022年第4期

612 2022 年 7 月

不同，两种模式会对损伤有不同的响应。一般来说，  l
p (t) = f(t),
 0
在相对低的频厚积范围内，S0 模式会有更快的传播 



 ∑
 2j−1 j
速度，而 A0 模式则相反 [12] 。复合材料是典型的各 p = H(k − 2t)p l−1 (t),

 l

 k
向异性材料，其各向异性特性受铺层、纤维材料属  2j ∑ j
p = G(k − 2t)p (t), (2)
性、树脂材料参数等影响，因此建模方法、频散曲线  l l−1

 k


求取等相比于各向同性材料更为复杂 [13−15] 。  l−1 ; j =1, 2, · · · , 2 ;
l
t=1, 2, · · · , 2






10 
L=log N,
2
A2 [ ]
8 A1 S1 p (t) = 2 ∑ h(t − 2k)p 2j−1 + ∑ g(t − 2k)p 2j ,
j
ᄱᤴए/(kmSs -1 ) 6 4 S0 其中，p 为第 l 层的第 j 个小波包系数，l 为分解层
l
l+1
l+1
k
k
(3)
j
l
2 A0 数，N 为信号长度；G、H 为小波包分解滤波器；g、h
为小波包重构滤波器。
0
0 1 2 3 4 5 6
Lamb 波是一种非平稳信号，而时频域分析法
ᮠԒሥ/(MHzSmm)
中小波包方法能够较好地逼近 Lamb 波信号，克服
(a) Lambฉᄱᤴएᮠஙజጳ
时域到频域中转换的不足。同时该方法对发现由于
10
损伤引起的 Lamb 波模式变换、频率变化等信息比
8 较有效，因此可以用来提高损伤评估的准确率。
Ꮖᤴए/(kmSs -1 ) 6 S0 A1 S1 2 损伤监测机理分析与特征提取
4
A2
A0
2.1 Lamb波响应信号的分析
2
复合材料的损伤形式多样，典型的损伤包括塑
0
0 1 2 3 4 5 6 性断裂、分层、裂纹、通孔和孔隙等。不同的损伤，其
ᮠԒሥ/(MHzSmm) 损伤特征也有所不同。结构损伤的发生，对Lamb波
(b) LambฉᏆᤴएᮠஙజጳ
响应信号的作用机理较为复杂，单纯地从时间域和
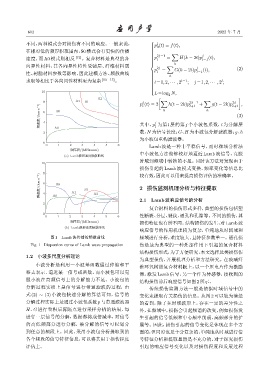
图 1 Lamb 波传播的频散曲线 频域进行分析，难度较大，且特征参数单一。通孔损
Fig. 1 Dispersion curve of Lamb wave propagation 伤是最为典型的一种外部作用下引起的复合材料
结构损伤形式，为了方便研究，本文选择此类损伤作
1.2 小波多尺度分析理论
为典型损伤，开展机理分析和方法研究。在玻璃纤
小波分析是利用一小波基函数通过伸缩和平
维环氧树脂复合材料板上，以一个压电片作为激励
移去表示、逼近某一信号或函数，而小波包可以克 器，激发 Lamb 信号，另一个作为传感器，接收到的
服小波在高频信号上的分解能力不足。小波包的 结构损伤前后响应信号如图2所示。
分解过程实质上是信号进行带通滤波的过程，由 传统损伤监测方法一般是依据时域信号中的
式 (2) ∼ (3) 小波包快速分解的算法可知，信号的 变化来提取有关损伤的信息。从图 2 可以较为清楚
分解过程实际上是通过小波包系数p 与带通滤波器 的看到，除了在时域波形上，存在一定的差异性之
H、G 进行卷积后再隔点进行采样分析的结果，每 外，在频域中，损伤会引起频谱的改变，例如损伤发
进行一层信号的分解，数据都将成倍减半，对信号 生引起的信号低频和中心频率削弱、高频部分的扩
的高低频部分进行分解，被分解的信号可以划分 展等。因此，损伤引起的信号变化是体现在多个方
到任意的频段上。因此，采用小波包分析提取到的 面的，但同时也是十分复杂的，单纯地从时域进行信
各个频段的信号特征信息，可以将其用于损伤程度 号特征分析和提取显然是不充分的，对于探究损伤
评估上。 引起的响应信号变化以及对损伤程度和发展过程