Page 195 - 《应用声学》2023年第3期

第 42 卷 第 3 期 孟子轩等： 基于非负矩阵分解的次声信号分类方法 633

图 5 中左侧为信号的字典矩阵，右侧为激活矩 量、时域熵、EMD能量、EMD熵等4 种特征，在上述
阵。结合图3 与图 5，可以看出字典矩阵是对信号时 实验条件下进行分类实验，分别使用 SVM 与一维
频谱的一种降维表示，不同类之间的字典矩阵有明 CNN作为分类器，其结果见表1。
显差异，因此本文选取 W 作为信号的特征向量进
18
行分类实验。 ஝૶ᝮै
16
લՌజጳ
2.2 实验环境 14
12
本文使用的数据集中训练集与测试集的比例
为7 : 3，由于数据量有限，因此不再设计验证集，而 ѣဘ൓஝ 10 8
是在训练时采用四折交叉验证的方式进行模型选 6
择。识别分类实验包括两部分，分别是基于经验模 4
态分解 (Empirical mode decomposition, EMD) 和 2
NMF 的识别分类实验。分类实验在 AMD®4600H 0 50 55 60 65 70 75 80 85 90
平台上进行，操作系统为 Windows10，所用软件为 юᆸဋ/%
Python3.6.8，CNN 的开发框架为 Tensorflow2.4.0，
图 6 HMS-SVM 测试集分类结果
SVM模型由Sklearn模块提供。
Fig. 6 Test set classification results of HMS-SVM
2.3 实验结果与分析
表 1 5 种特征分类结果
2.3.1 基于EMD的分类过程
Table 1 Five feature classification results
基于 EMD 的特征提取主要是对分解得到的各
阶本征模态函数(Intrinsic mode function, IMF) 分 使用特征 测试集准确率平均值/%
量进行处理 [3,5] ，可选择的处理方式包括计算分量 时域能量 67.78
各阶矩、能量、信息熵、波形特征、分量比等，经处 时域熵 58.06
理后的各分量仍可继续提取其能量、信息熵或波 EMD 能量 60.93
形特征等特征。本文采用时域能量、时域熵、EMD EMD 熵 68.73
能量、EMD 熵、EMD 奇异值以及希尔伯特边际谱 HMS 67.94
(Hilbert marginal spectrum, HMS) [21] 4 种特征作
从表 1 中可以看出，在本文所使用的数据集中，
为对比。以 HMS 为例，对识别分类过程进行说明。
5 种特征中最高的准确率为 EMD 熵特征，达到了
提取 HMS 时首先对时域信号进行 EMD，将得到的
68.71%。进行 EMD 后使用熵作为特征的准确率提
IMF进行希尔伯特变换，构造出原信号的解析信号，
升较高，而使用能量作为特征的准确率则有所下降。
从而得到原信号的希尔伯特谱，HMS 即为希尔伯
在进行实验前无法确定最优的特征提取方式，需
特谱的时间维积分结果，反映了瞬时频率的时域幅
要根据分类结果对特征向量进行设计以获取最佳
值累加。对得到的 HMS进行主成分分析 (Principal
特征。
component analysis, PCA)，取前30维作为SVM输
入进行分类。本文采取随机优化的方式对 SVM 进 2.3.2 基于NMF的分类过程
行参数选择，以相同条件进行100次分类实验，在测 使用 NMF 进行特征提取时，除字典原子个数
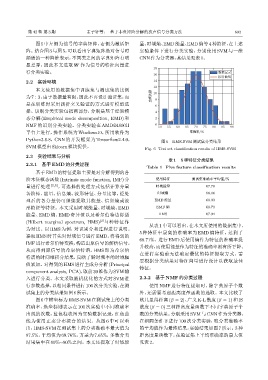
试集上的分类结果如图6所示。 外，还需要考虑距离度量函数的选取。本文比较了
图6中横坐标为HMS-SVM在测试集上的分类 欧几里得距离 (β = 2)、广义 K-L 散度 (β = 1) 和 IS
准确率，纵坐标则表示在 100 次实验中不同准确率 散度 (β = 0) 三种距离度量函数下不同字典原子个
出现的次数，蓝色柱状图为实验数据记录，红色曲 数的分类结果。分别采用SVM与CNN作为分类器，
线为使用正态分布拟合的结果。从图 6 中可以看 在相同条件下进行 100 次分类实验，取分类准确率
出，HMS-SVM 在测试集上的分类准确率最大值为 的平均值作为最终结果，实验结果如图 7 所示。3 种
87.5%，平均值为 69.76%，方差为 7.65%，多数分类 距离度量函数下，在验证集上平均准确率的最大值
结果集中在 60%∼80% 之间。本文还提取了时域能 见表2。