Page 224 - 《应用声学》2023年第3期

662 2023 年 5 月

1.3 呼吸声的倒谱系数计算 式(2)中，x (m)为经过预处理之后的声频离散序列，
声音频谱包络含有共振峰信息。而提取呼吸 X(k)为经过FFT变换的频域信号。
声的特征值重点就在于如何提取频谱包络 [10] 。频 (3) 对输入呼吸声所在的频域范围内设置一系
谱图反映的是整个声音信号的频谱分布，但是人耳 列的滤波器，这些滤波器组成 Mel 滤波器组。其滤
的听觉感知不是整个频谱范围，而是在某些特定的 波器的设置满足式(3)中的关系：
频谱范围。MFCC是最常见的语声特征。MFCC模
H m (k) =
拟了人耳的听觉特性，将原始频谱经过 Mel 频谱变 
换之后转化为基于 Mel 频谱的非线性频谱进行分 0, k < f(m − 1),



 k − f(m − 1)

析 [11] 。这样做的好处是对呼吸声信号进行降维，更 

 , f(m − 1) 6 k 6 f(m),
 f(m) − f(m − 1)
容易得到呼吸声信号的特征值 [12] 。 (3)

Mel 滤波器将信号的不同频率映射到 Mel 频  f(m + 1) − k

 , f(m) 6 k 6 f(m + 1),
f(m + 1) − f(m)

率，以此来模拟人耳的听觉系统。式(1) 是两者的变 


 0, k > f(m + 1),
换关系：
( )
f 式 (3) 中，k 指的输入信号的频谱分量，m指第 M 个
f Mel = 1125 × ln 1 + , (1)
700 滤波器，f(m) 指滤波器的中心频率。这里滤波器组
式 (1) 中，f 对应的是输入声音信号的频率，f Mel 表 个数m设置为26。
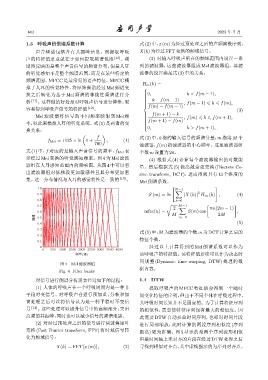
示经过 Mel 变换的听觉感知频率。图 4 为 Mel 滤波 (4) 根据式 (4) 计算每个滤波器输出的对数能
器组在人耳感知范围内的频响图。从图 4 中可以看 量。然后根据式 (5) 做离散余弦变换 (Discrete Co-
出滤波器组对低频段更加敏感并且其分布更加密 sine transform, DCT)，进而得到具有 13 个维度的
集。这一分布情况与人耳的感觉特性是一致的 [13] 。
Mel倒谱系数。
1.0 [ N−1 ]
∑
2
0.9 S (m) = ln |X (k)| H m (k) , (4)
0.8 k=0
0.7 √ M−1 [ ]
2 ∑ πn(2m − 1)
0.6 mfcc(n) = S(m) cos ,
ࣨϙ 0.5 M m=0 2M
0.4 (5)
0.3
式(5)中，M 为滤波器的个数，n为DCT计算之后的
0.2
特征个数。
0.1
0 经过以上计算得到的 Mel 倒谱系数可以作为
0 500 1000 1500 2000 2500 3000 3500 4000
ᮠဋ/Hz 该呼吸声的特征值。该特征值后续可以作为动态时
间规整 (Dynamic time warping, DTW) 处理的数
图 4 Mel 滤波器组
据内容。
Fig. 4 Filter banks
对信号进行倒谱分析需要经过如下的过程： 1.4 DTW
(1) 人体的呼吸声在一个呼吸周期内是一种非 提取呼吸声的 MFCC 特征值会得到一个随时
平稳时变信号。对呼吸声音进行预加重、分帧和加 间变化特征的序列，但由于不同个体在呼吸过程中，
窗处理之后可以将信号认为是一种平稳时不变信 其呼吸时间长短并不是固定的。为了计算特征序列
号 [14] 。这些处理可以提升信号中的高频部分，突出 的相似性，需要使特征序列保有最大的相似度。因
高频的共振峰，同时也可以减少信号的频谱泄露。 此需要 DTW 自动扭曲时间序列，也即对时间片段
(2) 对经过预处理之后的信号进行快速傅里叶 进行局部缩放，此时计算的两段序列相似度 (序列
变换 (Fast Fourier transform, FFT) 将时域信号转 距离) 更为准确。图 5 显示的是两个序列波形相似
化为频域信号： 但是时间轴上未对齐的片段在经过 DTW处理之后

X(k) = FFT [x (m)] , (2) 寻找到相似对齐点，其中虚线指示的为序列对齐点。