Page 45 - 《应用声学》2023年第4期

第 42 卷 第 4 期 梁鹏等： 三点弯曲试验条件下花岗岩声发射横纵波特征及损伤演化 707

100 100
ጫฉ˟ᮠӴඋ ഷฉ˟ᮠӴඋ
80 80
ጫฉ˟ᮠӴඋ/% 60 ഷฉ˟ᮠӴඋ/% 60

40
40
20 20

0 0
0 10 20 30 40 50 0 10 20 30 40 50
˟ᮠӝᫎ ˟ᮠӝᫎ
(a) ጫฉ (b) ഷฉ
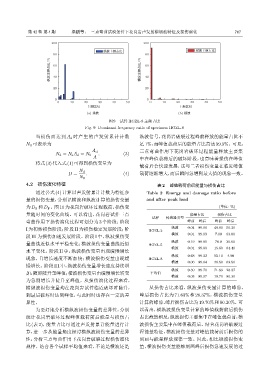
图 9 试件 HGZL-8 主频占比
Fig. 9 Dominant frequency ratio of specimen HGZL-8
当损伤面达到 A d 时产生的声发射累计计数 纵波信号，花岗岩破裂过程峰前释放的能量占比不
N d 可表示为 足1%，而峰值载荷后的能量占比高达 99.9%。可见，

A d 三点弯曲作用下花岗岩破坏过程能量释放主要集
N d = N s A d = N 0 . (3)
A 中在峰值载荷后的破坏阶段，也意味着损伤在峰值
将式(3)代入式(1)可得到损伤变量为
载荷后会快速发展，这与二者损伤变量在临近峰值
N d
D = . (4) 载荷逐渐增大，而后瞬间急增到最大值的现象一致。
N 0
4.2 损伤演化特征 表 2 峰值载荷前后能量与损伤占比

通过公式 (4) 计算以声发射累计计数为特征参 Table 2 Energy and damage ratio before
量的损伤变量，分别记横波和纵波计算的损伤变量 and after peak load
为D S 和D P 。图10为花岗岩破坏过程载荷、损伤变 (单位: %)
量随时间的变化曲线。可以看出，花岗岩试件三点 能量占比 损伤占比
试样 传感器类型
弯曲作用下损伤演化过程可划分为 3 个阶段：阶段 峰前 峰后 峰前 峰后
I 为初始损伤阶段；阶段 II 为损伤稳定发展阶段；阶 HGZL-2 纵波 0.04 99.96 49.80 50.20
横波 0.01 99.99 7.00 93.00
段 III 为损伤加速发展阶段。阶段 I 中，纵波损伤变
纵波 0.19 99.81 70.0 30.00
量曲线近似水平平稳变化；横波损伤变量曲线近似 HGZL-5
横波 0.01 99.99 15.60 84.40
水平变化。阶段 II 中，纵波损伤变量出现缓慢增长
纵波 0.68 99.32 95.10 4.90
现象，且增长速度不断加快；横波损伤变量出现缓 HGZL-8
横波 0.06 99.94 36.50 63.50
慢增长。阶段 III 中，纵波损伤变量增长速度持续增
纵波 0.30 99.70 71.63 28.37
加，随即陡升至峰值；横波损伤变量由缓慢增长转变 平均值
横波 0.03 99.97 19.70 80.30
为急剧增长并陡升至峰值。从损伤演化过程来看，
横纵波损伤变量均在花岗岩试件临近破坏时陡升， 从损伤占比来看，纵波损伤变量计算的峰前、
到最后破坏时达到峰值，与此同时也存在一定的差 峰后损伤占比为 71.63% 和 28.37%，横波损伤变量
异性。 计算的峰前、峰后损伤占比为19.70%和80.30%。可
为更好地分析横纵波损伤变量的差异性，分别 以看出，横纵波损伤变量计算的峰值载荷前后损伤
统计花岗岩破坏过程峰值载荷前后能量与损伤占 占比截然相反，纵波损伤主要集中在峰值载荷前，横
比 (表 2)，能量占比可通过声发射累计能量进行计 波损伤主要集中在峰值载荷后。结合花岗岩破裂过
算，进一步从能量角度探讨横纵波损伤变量的差异 程能量特征，横波损伤变量对峰值载荷前后损伤的
性，分析三点弯曲作用下花岗岩破裂过程损伤演化 刻画与能量释放规律一致。因此，相比纵波损伤变
规律。结合各个试样平均值来看，不论是横波还是 量，横波损伤变量能够刻画峰后损伤急速发展的过