Page 127 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 符晓磊等： Burst 模式在多波束声呐高帧率测深方法中的应用 1019

[ ]
H
2
其中，R x = E x(k)x(k) H = AR s A + σ I， 其中，ω 0 选用切比雪夫窗的权值作为具有低副瓣的
[ H ]
R s = E s(k)s(k) ，LCMV的准则方程为 模板权值，∥ ∥ 为欧几里得范数。ω 0 的方向图如图 7
所示。
H
min ω R x ω,
(6)
H
s.t. C ω = f, 0
-10
其中，C 为约束矩阵，f 为常量，通常，用拉格朗日乘
子法可得其最优解为 -20
H
(
ω opt = R −1 C C R −1 C ) −1 f. (7) ࣨए/dB -30
x
x
-40
LCMV 算法通过保证期望方向增益一定的条 -50
件下使系统输出功率最低，从而有效提高信号方向 -60
增益，同时抑制了干扰。设置期望信号方向为0 ，干 -70
◦
扰方向为 40 ，常规 LCMV 算法波束图如图 6 所示， -80
◦
-80 -60 -40 -20 0 20 40 60 80
可以看到干扰方向对应的零陷很窄，无法抑制具有 ᝈए/(°)
一定角度宽度的中央强信号的旁瓣干扰，而且副瓣
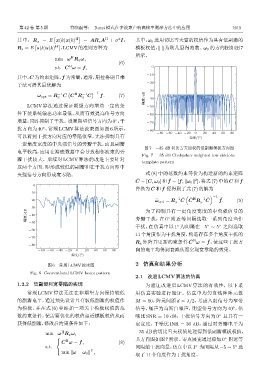
图 7 −35 dB 切比雪夫加权的低副瓣模板方向图
电平较高，应用在海底数据中会导致相邻波束的旁
Fig. 7 −35 dB Chebyshev weighted low sidelobe
瓣干扰较大。后续对 LCMV 算法的改进主要针对
template pattern
这两个方面，即形成较低的副瓣和在干扰方向即中
央强信号方向形成宽零陷。 式 (8) 中的范数约束等价为构造新的约束矩阵
˜
˜
2
C = [C, ω 0 ]和f = [f; ∥ω 0 ∥ ]，将式(7)中的C 和f
0
˜
˜
替换为C 和f 便得到了式(7)的解为
-10
( ) −1
˜
-20 ˜ ω opt = R −1 ˜ ˜ H −1 ˜ f. (9)
C C R
C
x
x
-30 为了抑制具有一定角度宽度的中央强信号的
ࣨए/dB -40 旁瓣干扰，在 0 附近等间隔选取一系列角度当作
◦
-50
干扰，在仿真中以 1 为间隔在 −5 ∼ 5 之间选取
◦
◦
◦
-60
11个角度作为干扰角度，构造存在多个角度干扰的
-70
˜
˜ H
R x 矩阵并更新约束条件 C ω = f，使这些干扰方
-80
-80 -60 -40 -20 0 20 40 60 80 向的电平均得到衰减从而实现宽零陷的效果。
ᝈए/(°)
图 6 常规 LCMV 波束图 2 仿真和结果分析
Fig. 6 Conventional LCMV beam pattern
2.1 改进LCMV算法的仿真
1.2.2 低副瓣和宽零陷的实现 为验证改进后 LCMV 算法的有效性，以下采
常规 LCMV 算法无法在非期望方向保持较低 用仿真实验进行验证。仿真中均匀直线阵阵元数
的副瓣电平，通过预先设计具有较低副瓣的权值作 M = 60，阵元间距 d = λ/2，考虑入射信号为窄带
为模板，并在式 (6) 中添加一项关于模板权值的范 信号，噪声为高斯白噪声，期望信号方向为 40 ，信
◦
数约束条件，使需要优化的权值逼近模板权值从而 噪比 SNR = 10 dB，干扰信号方向为 0 且具有一
◦
获得低副瓣，修改后约束条件如下： 定宽度，干噪比 INR = 30 dB，通过对旁瓣电平为
H
min ω R x ω, −35 dB的切比雪夫权值处理得到低副瓣模板权值，
 其方向图如图7所示。零点展宽通过添加0 附近等
◦
H
 C ω = f, (8)
s.t. 间隔的干扰向量，仿真中以1 为间隔从−5 ∼ 5 选
◦
◦
2
min ∥ω − ω 0 ∥ ,

取了11个角度作为干扰角度。