Page 166 - 《应用声学）》2023年第5期

1058 2023 年 9 月

随着信噪比的降低，伪峰会逐渐淹没在噪声的 30
背景高度中。对于双锥阵和螺线阵而言，二者的伪 25 ړಏ᫼
ԥ᩼᫼
峰本就较低，因此噪声的背景高度基本等同于最高 ᛃጳ᫼
伪峰高度，呈现出伪峰高度频响曲线随信噪比的降 20
低而升高的趋势；对于圆柱阵而言，其最高伪峰高度 AG/dB 15
本就很高，噪声背景高度仍无法将其淹没，因此其伪
10
峰高度频响曲线基本不随信噪比变化。
图 10 表明：双锥阵、螺线阵的伪峰高度显著 5
低于圆柱阵，例如在 SNR = 0 dB 的情况下，双锥
0
阵与螺线阵的最高伪峰高度分别约在 −10 dB 和 10 2 10 3 10 4
f/Hz
−15 dB，而圆柱阵平均在 −2 dB。图 11 表明：螺线
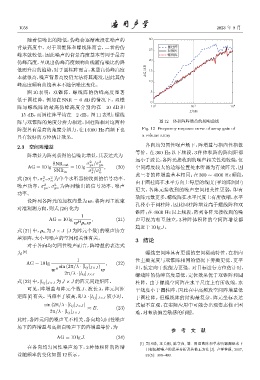
阵与双锥阵的角度分辨力相近，圆柱阵相对这两种 图 12 体积阵阵增益的频响曲线
阵型具有最高的角度分辨力，在14000 Hz 高频下也 Fig. 12 Frequency response curve of array gain of
具有较好的方位估计效果。 a volume array
各向均匀同性噪声场下，阵增益与指向性指数
2.3 空间阵增益
等价。在 300 Hz 以下频段，3 种体积阵的阵间距都
阵增益为阵列获得的信噪比增益，其表达式为
远小于波长，各阵元接收到的噪声相关性均较强，仅
2
SNR out σ /σ 2
ys
yn
AG = 10 lg = 10 lg , (20) 空间跨度较大的边缘位置处水听器为有效阵元，因
2
SNR in σ /σ 2
s n
此三者的阵增益基本相同；在 300 ∼ 4000 Hz 频段，
2
2
式(20) 中，σ 、σ 为单个水听器接收到的信号功率、 由于圆柱阵在水平方向上每层的线度(平均阵间距)
n
s
2
噪声功率，σ 、σ 2 yn 为阵列输出的信号功率、噪声 更大、各阵元接收到的噪声空间相关性更弱，即有
ys
功率。
效阵元数更多，螺线阵在水平尺度上有所收缩，水平
设阵列各阵元的加权向量为 w，将阵列主波束
孔径小于圆柱阵，因此圆柱阵增益高于螺线阵和双
对准观测方向，则式(20)化为
锥阵；在4000 Hz 以上频段，阵列各阵元接收到的噪
1
AG = 10 lg , (21) 声可视为相互独立，3 种阵体积阵的空间阵增益都
H
w ρ n w
趋近于10 lg J。
式 (21) 中，ρ n 为 J × J (J 为阵元个数) 的噪声协方
差矩阵，大小与噪声的空间相关性有关。 3 结论
对于各向均匀同性噪声而言，阵增益的表达式
为 [9] 螺线空间阵具有更强的空间稀疏特性，在指向
1 性主瓣宽度与双锥阵相同的情况下旁瓣更低、更平
AG = 10 lg , (22)
w H sin (2π/λ · [l ij ] J×J ) w 坦，抗定向干扰能力更强。对目标进行方位估计时，
2π/λ · [l ij ] J×J
螺线阵的伪峰高度最低，定位效果优于双锥阵和圆
式(22)中，[l ij ] J×J 为J × J 的阵元间距矩阵。 柱阵。由于螺线空间阵在水平尺度上有所收缩，水
可见，阵增益与阵元个数 J、波长 λ、阵元间距 平线度小于圆柱阵，因此在中高频段空间阵增益低
矩阵[l]有关。当频率f 较高，即λ · [l ij ] J×J 较小时， 于圆柱阵。但螺线阵的结构最复杂、阵元坐标表达
sin (2π/λ · [l ij ] J×J ) 式最不直观，在实际应用中可能会出现姿态修正困
≈ E. (23)
难、对布放偏差敏感的问题。
2π/λ · [l ij ] J×J
此时，各阵元间的噪声互不相关，各向均匀同性噪声
场下的阵增益与高斯白噪声下的阵增益等价，为
参 考 文 献
AG = 10 lg J. (24)
[1] 吴国清, 王美刚, 陈守虎, 等. 用垂直阵和单水听器测量水下
在各向均匀同性噪声场下，3 种体积阵的阵增
目标辐射噪声的误差分析及其修正方法 [J]. 声学学报, 2007,
益随频率的变化如图12所示。 32(5): 398–403.