Page 139 - 《应用声学》2024年第1期

第 43 卷 第 1 期 周峻林等： 合成语声的声学分析及识别特征算法 135

自动化识别合成语声。本节针对声学比对结果，对 号的真实强度大小，有利于提取出周期性变化的语
不同的声学特性差异开展了特征量化，设计选用不 声信号的每一帧能量，而每一帧的语声能量有效值
同的声学特征及其结合开展实验，以验证性能。 则能够较好地表征出信号在较短时间段内的能量
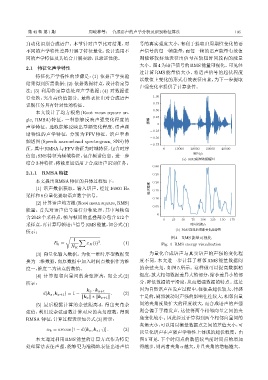
大小。图4为语声信号的RMS能量可视化。可见经
2.1 特征化声学特性
过计算 RMS 能量值大小，将语声信号的起伏程度
特征化声学特性的步骤是：(1) 依据声学实验
以数值上变化的形式有效表征出来，为下一步提取
结果得到所需数据；(2) 依据数据特点，设计特定算
声强变化率提供了计算条件。
法；(3) 利用特定算法处理声学数据；(4) 对数据进
行变换，突出高价值部分。最终表征出对合成语声 1.00
识别任务具有针对性的特征。 0.75
0.50
本文设计了均方根角 (Root mean square an-
0.25
gle, RMSA) 特征，一种能够反映声强变化程度的 ૝ࣨ
声学特征。选取能够反映出基频变化程度、语声频 0
-0.25
谱特性的声学特征，分别为 FFV 特征、语声窄带
-0.50
频谱图 (Speech narrowband spectrogram, SNS) 特
-0.75
征。其中RMSA与FFV特征为时域特征，包含时序 0 10000 20000 30000 40000
௑ᫎ/s
信息；SNS 特征为频域特征，包含频谱信息。进一步
(a) RMSᑟ᧚ᄊ૝ࣨڏ
结合3种特征，将能更加适用于合成语声识别任务。
0.30
2.1.1 RMSA特征 0.25

本文提出RMSA特征的具体过程如下： 0.20
(1) 语声数据获取。输入语声，经过 16000 Hz ᡑ͒ሮए 0.15
采样和8位量化提取语声数字信号。
0.10
(2) 计算语声均方根(Root mean square, RMS)
0.05
能量。首先对语声信号进行分帧处理，其中每帧包
0
含 2048 个采样点，帧与帧间的重叠部分包含 512 个
0 25 50 75 100 125 150 175
采样点，再计算每帧语声信号RMS能量，如公式(1) ௑ᫎևర/s
所示： (b) RMSᑟ᧚ᄊևరԫӑᡖҹڏ
√ 图 4 RMS 能量可视化
1 ∑ 2
E k = x K (i) . (1) Fig. 4 RMS energy visualization
N K
(3) 向量化输入数据。为使一维时序型数据变 为量化合成语声与真实语声的声强的变化程
换为二维数据，向原数据中加入时间点数据作为维 度不同，本文进一步计算了相邻 RMS 能量数据间
度一，维度二为该点的数值。 的余弦夹角，如图 5 所示。这样做可以提高数据精
(4) 计算相邻向量间的余弦距离，如公式 (2) 细度，放大相邻数据差异大的部分，缩小差异小的部
所示： 分，降低数据的平滑度，从而增强数据的特点。这是
因为自然语声在发声过程中，往往是起伏较大、律感
k x · k x+1
d(k x , k x+1 ) = 1 − . (2)
∥k x ∥ ∗ ∥k x+1 ∥ 十足的，剧烈波动对声强的影响往往较大，相邻向量
(5) 最后根据计算的余弦距离 d，得出夹角余 间的夹角度数扩大的程度较大，而合成语声的声强
弦值，利用反余弦函数计算对应的夹角度数，得到 则会偏于平稳发声，这使得两个相邻向量之间的夹
RMSA 特征，计算过程表示如公式(3)所示： 角变化较小。因此经过计算得到两个相邻向量间的
夹角大小，可以用以衡量数据点之间的差值大小，可
α k = arccos [1 − d (k x , k x+1 )] . (3)
以量化语声在声强声学特性上体现的起伏程度。由
本文通过利用 RMS 能量的计算方式作为特定 图 5 可见，下个时间点的数值较当前时间点的增加
处理算法表征声强，能够更为准确地表征出语声信 得越多，则两者夹角α 越大，并且夹角的增幅越大。