Page 8 - 《应用声学》2024年第6期

1184 2024 年 11 月

动量守恒以及物态方程，具体如下 [13] ： 发产生的声波能量呈周期性交替变化。频率较低的
∂ 声波在传播过程中声压变化相对较小，且声波的振
(ρ) + ∇ · (ρU i ) = 0, (10)
∂t 动周期较长，单个周期内传输的能量较少。而频率
∂
(ρU i ) + ∇ · (ρU i U j ) = − ∇p + ∇ · σ, (11) 较高的声波在传播过程中声压变化相对较大，声波
∂t
ρ = ρ(p, T), (12) 的振动周期较短，每个周期内传输的能量较多。因
此，声波驱动产生的近声场能量随着声波频率的增
其中，ρ 为空气密度；U i 、U j 为脉动速度分量；p 为压
大呈逐渐增大的趋势。由图 4 可以看出，在声源上
力；σ 为黏性应力；T 为温度。
方，声压级的分布达到整个区域的极大值，在声源侧
结合式 (10)∼ 式 (12) 以及 N-S 方程，构建声场
方区域，随着距离声源越来越远，声场强度呈逐渐减
与湍流场耦合的基本控制方程为
弱的趋势，但是随着加载的声波频率的增大，声波的
( )
1 dP 0 dP rms
+
ρ dz dz 扰动范围呈逐渐增大的趋势。
2
2 d ( d U 1 1 dU 1 ) 当声波在空气中传播时，考虑到湍流黏性对
= − (rK) + v +
3r dr dr 2 r dr 声波能量的耗散效应，当加载的声波驱动频率
2
( )
d U rms 1 dU rms f = 1200 Hz，选择水平和垂直特征截面上不同入射
+ v + , (13)
dr 2 r dr
压力下一个声波驱动周期内声压级的变化进行研
式(13) 中，K 为湍流平均动能；v 为运动黏度；U 1 表 究。由图 5 可以看出，随着声波入射压力幅值的增
¯
示整个风场前方来流速度 U 1 = U 0 + U(z)，其中
大，整个区域内声场能量呈现逐渐增大的趋势。由
¯
U(z)表示近地面层梯度风速。
图 5(a) 可知，在水平截面声源正上方声压级变化剧
烈，达到整个区域的极大值，随着距离声源越来越
2 数值计算及结果分析
远，声波辐射能量场逐渐减弱，声压级呈现波动减小
2.1 声波辐射的声场能量分布 的趋势；由图 5(b)可知，在声源垂直截面正上方，随
在地表温度恒定的情况下，对不同声波参数情 着距离地面的高度增大，由大气湍流黏性效应引起
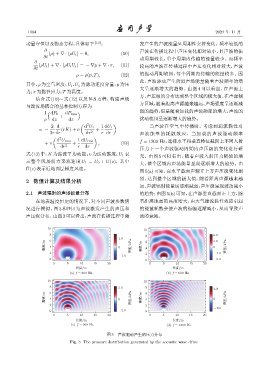
况进行模拟，图 3 和图 4 为声波激发产生的声压和 的能量耗散会使声波的振幅逐渐减小，从而导致声
声压级分布。由图3可以看出，声波在传播过程中激 波的衰减。

10
10
8 8 2.0
1.0 1.0
6
ᰴए/m 4 0 ܦԍ/kPa ᰴए/m 6 4 0 ܦԍ/kPa
2 2 -1.0
-1.0
0 0 -2.0
0 5 10 15 20 0 5 10 15 20
᫂ए/m ᫂ए/m
(a) f=300 Hz (b) f=600 Hz
10 10
8 2.0 8
2.0
6
ᰴए/m 4 0 ܦԍ/kPa ᰴए/m 6 4 0 ܦԍ/kPa
2 2
-2.0
0 -2.0 0
0 5 10 15 20 0 5 10 15 20
᫂ए/m ᫂ए/m
(c) f=900 Hz (d) f=1200 Hz
图 3 声波驱动产生的压力分布
Fig. 3 The pressure distribution generated by the acoustic wave drive