Page 157 - 《应用声学》2025年第2期

第 44 卷 第 2 期 李赶先等： 海底沉积物纵波声速随孔隙度变化的物理机制 417

沉积物孔隙度增大，其密度减小。由于介质密度对 Orsi等 [31] ：
其弹性性质产生重要影响，所以，海底沉积物孔隙度 2 4 2
C p = 2527 − 27.132 × 10 n + 0.1782 × 10 n
变化引起密度变化，将导致沉积物纵波声速发生响
(大陆架、大陆坡). (7)
应变化。
由以上结果可见，在海底沉积物纵波声速随孔 唐永禄 [32] ：
隙度变化过程中，同时发生着含水量、中值粒径和 2 4 2
C p = 942 + C 0 − 25.02 × 10 n + 0.156 × 10 n
密度等参数随孔隙度相关变化，这反映出海底沉积
(南海北部大陆架), (8)
物纵波声速与孔隙度的响应变化存在着含水量、中
值粒径和密度等物理参数的影响，深入分析这些物 式 (8) 中，C 0 为海水声速；分析时取 C 0 = 1529.8
理参数在海底沉积物纵波声速随孔隙度变化中的 m·s −1 (相当于Hamilton的测量现场)。
作用效应，对于揭示海底沉积物纵波声速变化的物 卢博等 [33] ：
理机制具有重要意义。 2 4 2
C p = 2369.07 − 25.53 × 10 n + 0.185 × 10 n
(中国东南沿海近海). (9)
3 海底沉积物纵波声速最小值的发现及其
统一分析 上述学者得到的不同海区海底沉积物纵波声
速(C p ，m·s −1 )与孔隙度(n)经验公式的参数相关曲
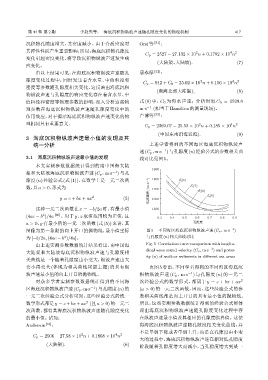
3.1 海底沉积物纵波声速最小值的发现 线对比见图5。
本文实测参数数据统计得到的南中国海大陆
1900
架和大陆坡海底沉积物纵波声速 (C p ，m·s −1 ) 与孔
隙度 (n) 经验公式 (式 (1))，在数学上是一元二次函 1800 र(6)
数，且a > 0，形式为 ጫฉᤴܦ/(mSs -1 ) 1700 र(7) र(8)

2
y = c + bx + ax . (5) 1600 र(9)
这种一元二次函数在 x = −b/2a 时，有最小值 1500
2
(4ac − b )/4a [30] 。对于 y、x 取值范围均为正值，且 0.3 0.4 0.5 0.6 0.7 0.8 0.9
a > 0、y 有最小值的一元二次函数 (式 (5)) 来讲，其 ߘᬩए
图像为第一象限的向上开口的抛物线，最小值坐标 图 5 不同海区海底沉积物纵波声速 (C p，m·s −1 )
2
为[−b/2a, (4ac − b )/4a]。 与孔隙度 (n) 相关曲线对比
由上述实测参数数据统计结果看出，南中国海 Fig. 5 Correlation curve comparison with longitu-
dinal wave sound velocity (C p, m·s −1 ) and poros-
大陆架和大陆坡海底沉积物纵波声速与孔隙度相
ity (n) of seafloor sediments in different sea areas
关曲线是一个随着孔隙度由小变大，纵波声速由大
变小再变大 (体现为相关曲线尾部上翘) 的具有纵 由图 5 看出，不同学者得到的不同海区海底沉
波声速最小值的向上开口的抛物线。 积物纵波声速 (C p ，m·s −1 ) 与孔隙度 (n) 的一元二
对众多学者实测参数数据统计得到的不同海 次经验公式的数学形式，都属于 y = c + bx + ax 2
区海底沉积物纵波声速(C p ，m·s −1 )与孔隙度(n)的 (a > 0) 的一元二次函数，因而，这些经验公式的参
一元二次经验公式分析可知，这些经验公式的统一 数相关曲线都是向上开口的具有最小值的抛物线。
数学形式都是y = c + bx + ax (且a > 0)的一元二 所以，这些实测参数数据统计得到的经验公式都体
2
次函数，都有其海底沉积物纵波声速随孔隙度变化 现出海底沉积物纵波声速随孔隙度变化过程中存
的最小值。诸如： 在纵波声速最小值及其相应的孔隙度临界值。这使
Anderson [18] ： 得海底沉积物纵波声速随孔隙度相关变化曲线，并
不是单调下降或者单调上升，而是在孔隙度由小变
2
4 2
C p = 2506 − 27.58 × 10 n + 0.1868 × 10 n
大的过程中，海底沉积物纵波声速在相对低孔隙度
(大陆架). (6)
阶段随着孔隙度增大而减小，当孔隙度增大到某一