Page 36 - 201901

32 2019 年 1 月

分主要由线圈的直流阻构成，随着频率增加感抗增 和另一端的鼓膜形成了密闭的腔体空间，该空间内
加；3.5 kHz 附近为动圈结构的共振频率，在该峰值 空气共振改变了耳道负载阻抗。图 6 中电阻抗曲线
处满足 第三个共振峰位于 8.6 kHz 左右，对应于人工头耳
√ [23]
1 1 道封闭时的3/4波长共振频率 ：
f s = . (1)
2π M m C m c
f c = , n = 1, 3, 5... (3)
第二个共振峰出现在 6.7 kHz 附近，是前腔内空气 n · 1/4λ
发生共振的频率。与式(1)类似，振动频率与空气的 其中，λ 为 12 cm，对应于人工耳 3 cm 长度的 4 倍。
等效声顺和等效质量有关。其中当封闭管中空气容 耳道原有的 1/4波长共振峰由于入耳式耳机机械阻
积为V 时，管中空气的声顺与容积成正比： 抗的影响没有得到清晰地体现。仿真电阻抗曲线由
V 于依赖集总参数模型因而受到低频假设的限制，因
C a = . (2)
ρ 0 c 2 0 此超过 7 kHz 的部分无法准确描绘耳机工作时的参
大于 6.7 kHz 的高频段内，音圈感抗的成分随 数表现。这里应该强调满足低频假设频段内，耳机
频率增加迅速上升，电阻抗曲线随频率上扬。 电阻抗曲线在空负载与塞入耳道两种状态之间的
变化：第二个共振峰移动到 5.9 kHz 附近，对应于耳
s↼t↽ D/A p↼t↽ 机封闭耳道所形成腔体的共振频率。
Z e
ႃ᫾
V 1↼t↽ Ԫភ٨ 18.4
18.3
V 2↼t↽ ࠄᬅ฾᧚
Z↼t↽ A/D 18.2 വی͌ᄾ
18.1
ႃ᫾ઈ/W 17.9
18.0
图 4 耳机电阻抗测量框图 17.8
Fig. 4 The schematic of electric impedance mea- 17.7
surement 17.6
17.5
17.4
18.6 10 2 10 3 10 4
ᮠဋ/Hz
18.4
ࠄᬅ฾᧚
വی͌ᄾ 图 6 耳机与外耳耦合电阻抗实验测量结果与仿真
18.2 结果对比
ႃ᫾ઈ/W 18.0 Fig. 6 Comparison of measurement and simula-

17.8 tion impedance curves of loaded earphone
1.3 传递路径分析
17.6
利用声学类比线路图可以计算得到入耳式耳
17.4
10 2 10 3 10 4 机的幅频响应曲线，即图 3 中箭头所指 p 处相对于
ᮠဋ/Hz
接地点的声压。为了验证模型的准确性，采用人工
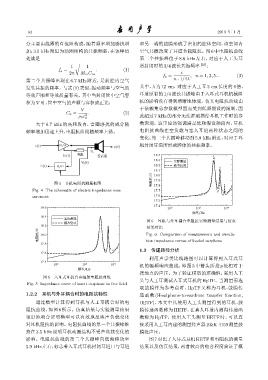
图 5 入耳式耳机自由辐射电阻抗曲线
头与人工耳测试入耳式耳机的 HpTF。当测量需选
Fig. 5 Impedance curve of insert earphone in free field
取鼓膜作为参考点时，HpTF 又称为耳机 -鼓膜传
1.2.2 耳机与外耳耦合时的电阻抗特性 递函数 (Headphone-to-eardrum transfer function,
通过模型计算得到耳机与人工耳耦合时的电 HETF)，本文中凡使用人工头测量得到的耳机 -鼓
阻抗曲线，如图 6 所示。仿真结果与实验测量结果 膜传递函数称为 HETF，在真人耳道内测得传递函
很好地吻合证明模型可以有效地反映声负载变化 数称为 HpTF。使用人工头测量 HETF 时，可以直
对耳机阻抗的影响。电阻抗曲线的第一个共振峰维 接采用人工耳内建的测量传声器B&K 4159测量鼓
持在 3.5 kHz 说明耳机动圈结构不受声负载变化的 膜处声压。
影响。电阻抗曲线的第二个共振峰向低频移动至 图7对比了入耳式耳机HETF和电阻抗的测量
5.9 kHz左右，标志着入耳式耳机封闭耳道口与耳道 结果以及仿真结果，两者较高的吻合程度验证了模