Page 69 - 201901

第 38 卷 第 1 期 郭颖等： 偏度最大化多通道逆滤波语声去混响研究 65

2.1.3 高斯噪声环境下算法鲁棒性 在高斯白噪声环境下，影响本文算法去混响性
该实验测试本文提出算法在加性高斯白噪声 能的因素有如下两个方面：一方面，当信号信噪比过
环境下的去混响性能。用PESQ得分和语声-混响调 低时，会引起线性预测模型谱密度产生畸变，使谱估
制能量比 (Speech-to-reverberation modulation en- 计的质量受到损失，LP系数的估计变得不准确。另
ergy ratio, SRMR) [21] 作为评价指标。 一方面，加性噪声的存在使信号的概率密度分布更
图5 给出了对RT 60 = 400 ms 时的传声器阵列 趋于高斯分布，会改变自适应滤波过程中高阶统计
信号加入不同信噪比的高斯白噪声，逆滤波后的 量局部极大值点的位置，相比于没有噪声的情况使
信号平均 PESQ得分和平均SRMR。峰度算法对信 目标函数收敛到次极大值点，从而降低逆滤波的性
能。提出的偏度方法相较于峰度方法对高斯噪声的
噪比低于 20 dB 输入信号失效，对房间脉冲响应
鲁棒性更强，其原理可以通过以带有加性噪声的信
的逆滤波无法得到单一峰值的结果；本文提出的
号作为输入，计算两种算法的梯度来直观解释。峰
MLPRS 算法对低于 10 dB 的输入信号失效，但去
度方法的梯度中受加性噪声影响的项更多，不稳定
混响效果明显优于峰度方法；而采用联合估计的
因素更多，因此峰度方法相比于偏度方法对加性噪
MSJE算法对测试的所有信噪比下的数据都能达到
声更加敏感。MSJE 方法采用预测误差滤波器与房
比较好的效果。本文提出的基于偏度的多通道逆滤
间脉冲响应逆滤波器的联合估计方法，使 LP 系数
波方法在高斯白噪声环境下的去混响性能比已有
的估计更为准确，减弱了上述第一个因素的影响，因
的基于峰度的多通道逆滤波方法有很大提升，提出
此相较于 MLPRS 方法对噪声的鲁棒性更强一些，
方法对高斯噪声的鲁棒性更强。
在信噪比较低的情况下能更准确地估计逆滤波器。
2.6 MSJE 2.1.4 计算复杂度
2.4 MLPRS
࢏एካข
2.2 采用峰度和偏度准则的计算复杂度差别主要
ຉ־
2.0 体现在梯度上，基于偏度准则的更新梯度表示为公
PESQ 1.8 式(17)，峰度准则的更新梯度可以进行类似的推导，
1.6
最终表示为
1.4
∂Q (n)
′
1.2
r
∂g m
1.0 ( { } { } )
2
4
3
0 5 10 15 20 Inf d (n)E d (n) − d i (n)E d (n)
i
i
i
≈ 4 · r mi (n)
SNR/dB 3 2
E {d (n)}
i
(a) PESQ४Ѭ
′
= q (n) · r mi (n). (21)
4.0
在计算梯度过程中 q (n) 相比于 q(n) 在计算时多一
′
3.5 次乘法，因此偏度方法相比于峰度方法计算量更低。
SRMR/dB 3.0 另一方面，表 1 给出了两种算法在不同混响时间情
况下所需的最小滤波器阶数，偏度算法所需的滤波
2.5
MSJE 器阶数更少，也同时降低了算法的计算复杂度。
2.0 MLPRS
࢏एካข
1.5 2.2 实际环境录音仿真测试
ຉ־
0 5 10 15 20 Inf 为了更合理地评估提出算法的去混响性能，本
SNR/dB
实验采用实际环境录音的多通道房间脉冲响应数
(b) SRMR
据库 [22−23] 与 TIMIT 数据库的 20 s 纯净语声信号
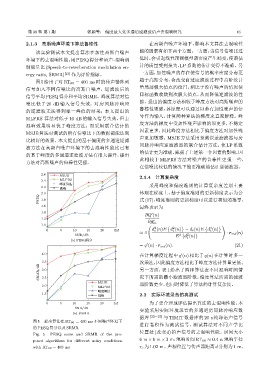
图 5 提出算法在 RT 60 = 400 ms 不同噪声环境下
进行卷积作为测试信号，测试算法对不同声学比
的 PESQ 得分以及 SRMR
位置处 (改变 d) 拾声信号的去混响性能。房间大小
Fig. 5 PESQ score and SRMR of the pro-
posed algorithms for different noisy conditions 6 m × 6 m × 3 m，混响时间RT 60 ≈ 0.4 s，混响半径
with RT 60 = 400 ms r c 为1.02 m。声源位置与传声器距离 d分别为 1 m、