Page 16 - 应用声学2019年第2期

162 2019 年 3 月

20 因此，上述的57阶FIR和12阶IIR滤波器直接
IIR
0
FIR I 型实现时的运算量如表 2 所示，其中，输出序列长
-20 度N y = 16384，输入序列长度N x = 16384 + N − 1。
ܙᄞ/dB -40 由此看出，理论上，前者的运算量约是后者的 2
-60
-80 倍多。
表 2 FIR 和 IIR 运算量理论值
-100
Table 2 Amount of calculation comparison
-120
0 5 10 15 20 25 between FIR and IIR
ᮠဋ/MHz

图 2 IIR 和 FIR 滤波器幅频特性曲线 乘法次数 乘法次数之比 加法次数 加法次数之比
Fig. 2 Amplitude-frequency curves of IIR and 57 阶 FIR 16384×58 16384×57
2.32 2.37
FIR filters 12 阶 IIR 16384×25 16384×24

0.2
1.0
ᣥКηՂ
FIR FRR
0.1
0.5
ॆʷӑࣨए 0
ᘿᦊ 0

-0.1
-0.5
-0.2
-1.0 0.026 0.028 0.030 0.032 0.034 0.036
-1.0 -0.5 0 0.5 1.0 t/ms
ࠄᦊ (a) FIR FRR
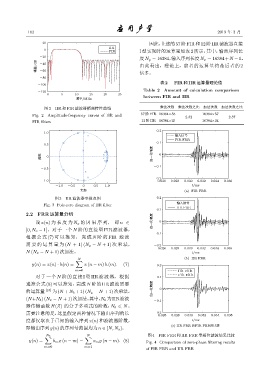
图 3 IIR 滤波器零极点图 0.2
Fig. 3 Pole-zero diagram of IIR filter ᣥКηՂ
IIR FRR
0.1
2.2 FRR运算量分析
ॆʷӑࣨए 0
设 x(n) 为 长 度 为 N x 的 因 果 序 列， 即 n ∈
[0, N x − 1]。对于一个 N 阶的直接型 FIR 滤波器，
-0.1
根 据 公 式 (7) 可 以 推 知， 完 成 N 阶 的 FIR 滤 波
需 要 的 运 算 量 为 (N + 1) (N x − N + 1) 次 乘 法， -0.2
0.026 0.028 0.030 0.032 0.034 0.036
N (N x − N + 1)次加法。 t/ms
N (b) IIR FRR
∑
y(n) = x(n) · h(n) = x (n − m) h (m). (7) 0.2
m=0 IIR FRR
对于一个 N 阶的直接 I 型 IIR 滤波器，根据 0.1 FIR FRR
递推公式 (8) 可以推知，完成 N 阶的 IIR 滤波需要
的运算量 [13] 为(N + N b + 1) (N x − N + 1)次乘法， ॆʷӑࣨए 0
(N+N b ) (N x − N + 1)次加法。其中，N b 为IIR滤波
-0.1
器传输函数 H(Z) 的分子多项式的阶数，N b 6 N。
需要注意的是，这里假定两种情况下输出序列的长 -0.2
0.026 0.028 0.030 0.032 0.034 0.036
度都仅取决于已知的输入序列 x(n) 和滤波器阶数， t/ms
(c) IIR FRR ބFIR FRR֥бࢠ
即输出序列y(n)的序列号范围均为n ∈ [N, N x ]。
N 图 4 FIR FRR 和 IIR FRR 零相位滤波结果比较
N b
∑ ∑
y(n) = b m x (n − m) − a m y (n − m). (8) Fig. 4 Comparison of zero-phase filtering results
m=0 m=1
of FIR FRR and IIR FRR