Page 58 - 应用声学2019年第5期

810 2019 年 9 月

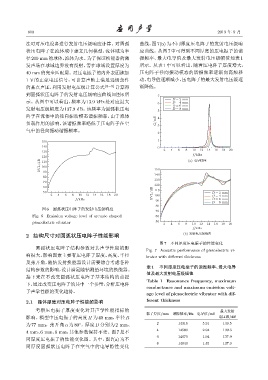
法可对压电设备进行发射电压级响应计算。对圆弧 曲线，图 7(b) 为不同厚度压电阵子的发射电压级响
状压电阵子在流体域中建立几何模型，流体域为半 应曲线。从图 7 中可得到不同厚度的压电振子的谐
径200 mm的球体，流体为水。为了保证换能器的激 振频率、最大电导值及最大发射电压级幅值如表 1
发声场在球域边界没有反射，需在球域设置厚度为 所示。从表 1 中可以看出，随着压电阵子厚度增大，
40 mm的完全匹配层。对压电振子的内外表面施加 压电阵子径向振动模态的谐振频率逐渐向高频移
1 V 的正弦电压信号，可计算声轴上满足远场条件 动，电导值逐渐减小，压电阵子的最大发射电压级逐
的某点声压，利用发射电压级计算公式 [8−9] 计算得 渐降低。
到圆弧状压电阵子的发射电压级响应曲线如图6 所 7
D=2 mm
示。从图中可以看出，频率为 13.9 kHz 处对应最大 6 D=4 mm
D=6 mm
发射电压级幅度为 137.9 dB。该频率为圆弧状压电 5 D=8 mm
阵子在流体中的径向振动模态谐振频率，由于流体 4
负载作用的影响，该谐振频率略低于压电阵子在空 G/mS 3
气中的径向振动谐振频率。
2
150 1
140 0
2 4 6 8 10 12 14 16 18 20
130
f/kHz
120 (a) ႃ࠮ྲভ
SVL/dB 110 150
100
90
140
80
130
70
120
60
50 SVL/dB 110 D=2 mm
2 4 6 8 10 12 14 16 18 20 100 D=4 mm
f/kHz 90 D=6 mm
D=8 mm
80
图 6 圆弧状压电阵子的发射电压级响应
70
Fig. 6 Emission voltage level of arcuate shaped 60
piezoelectric vibrator 50 2 4 6 8 10 12 14 16 18 20
f/kHz
2 结构尺寸对圆弧状压电阵子性能影响 (b) ԧ࠱ႃԍጟ־ऄ

图 7 不同厚度压电振子的性能变化
圆弧状压电阵子结构参数对其声学性能的影
Fig. 7 Acoustic performance of piezoelectric vi-
响很大，影响因素主要有压电阵子厚度、高度、半径 brator with different thickness
及张开角，随钻发射换能器设计需要综合考虑各种
表 1 不同厚度压电振子的谐振频率、最大电导
结构参数的影响，设计满足随钻测量环境的换能器。
值及最大发射电压级幅值
接下来在不改变圆弧状压电阵子基本结构的前提
Table 1 Resonance frequency, maximum
下，通过改变压电阵子的其中一个参量，分析压电阵
conductance and maximum emission volt-
子声学性能的变化趋势。
age level of piezoelectric vibrator with dif-
2.1 晶体厚度对压电阵子性能的影响 ferent thickness
考察压电振子厚度变化对其声学性能指标的 最大发射
振子厚度/mm 谐振频率/Hz 电导值/mS
影响。模型中压电振子的高度 H 为 40 mm，半径 R 电压级/dB
为 77 mm，张开角 α 为 80 ，厚度 D 分别为 2 mm、 2 14316 5.91 143.5
◦
4 mm、6 mm、8 mm，其他参数保持不变。图7 是不 4 14500 2.94 139.3
6 14670 1.94 137.9
同厚度压电振子的性能变化图。其中，图 7(a) 为不
8 14840 1.45 137.3
同厚度圆弧状压电阵子在空气中的电导特性变化