Page 70 - 《应用声学》2020年第2期

228 2020 年 3 月

3.4 实验分析 表 3 列出了本文提出的两种声学模型实验结
为验证提出的 MCNN-CTC 以及 SE-MCNN- 果，其中 MCNN(7)-CTC 表示 MCNN 层数为 7 层；
CTC 声学模型的性能，在 Thchs30 以及 ST-CMDS SENet 模型在 7 层 MCNN 模型上进行改进，其中
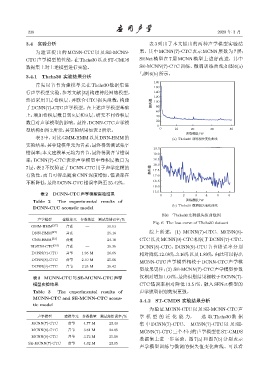
数据集上对上述模型进行实验。 SE-MCNN(7)-CTC 训练、微调训练曲线如图 6(a)
与图6(b)所示。
3.4.1 Thchs30 实验结果分析
180
首先以音节为建模单元在 Thchs30 数据集进
160
行声学模型实验，参考文献 [32] 构建神经网络模型， 140
120
然后采用 7 层卷积层，并联合 CTC 损失函数，构建 100
了DCNN(7)-CTC 声学模型。在上述声学模型基础 ૯ܿϙ 80
60
上，增加卷积层数目到 8 层和 9 层，研究不同卷积层 40
数目对声学模型的影响。最终，DCNN-CTC声学模 20
0
型结构如图2所示，其实验结果如表2所示。 0 10 20 30 40
ᝫጷ஝૶/W
表 2 中，对比 GMM-HMM 以及 DNN-HMM 的 (a) Thchs30 ᝫጷ૯ܿԫӑజጳ
实验结果，其中建模单元为音素，最终得到测试集字
19.5
错误率；本文建模单元均为音节，最终得到音节错误 19.0
率；DCNN(7)-CTC 表示声学模型中卷积层数目为 18.5
7 层，表 2 不仅验证了 DCNN-CTC 用于声学建模的 ૯ܿϙ 18.0
17.5
有效性，而且可得出随着 CNN 深度增加，错误率在 17.0
不断降低，最终DCNN-CTC错误率降至25.42%。 16.5
16.0
15.5
表 2 DCNN-CTC 声学模型实验结果 0 1 2 3 4 5 6
Table 2 The experimental results of ᝫጷ஝૶/W
(b) Thchs30 ॲូ૯ܿԫӑజጳ
DCNN-CTC acoustic model
图 6 Thchs30 实验损失值曲线图
声学模型 建模单元 参数数量 测试集错误率/%
Fig. 6 The loss curve of Thchs30 dataset
GMM-HMM [27] 音素 — 30.53
DNN-HMM [27] 音素 — 25.16 综上所述：(1) MCNN(7)-CTC、MCNN(8)-
CNN-HMM [33] 音素 — 24.10 CTC 以及 MCNN(9)-CTC 相较于 DCNN(7)-CTC、
BLSTM-CTC [34] 音素 — 25.35 DCNN(8)-CTC、DCNN(9)-CTC 音节错误率分别
DCNN(7)-CTC 音节 1.95 M 26.65 相对降低 12.08%、3.16%以及 1.89%，由此可以得出
DCNN(8)-CTC 音节 2.10 M 25.66
MCNN-CTC 声学模型相较于 DCNN-CTC 声学模
DCNN(9)-CTC 音节 2.25 M 25.42
型效果更佳；(2) SE-MCNN(7)-CTC 声学模型参数
表 3 MCNN-CTC 与 SE-MCNN-CTC 声学 仅相对增加1.04%，最终识别结果相较于DCNN(7)-
模型实验结果 CTC 错误率相对降低 13.51%，融入 SENet 模型的
Table 3 The experimental results of 声学模型识别效果更强。
MCNN-CTC and SE-MCNN-CTC acous-
3.4.2 ST-CMDS 实验结果分析
tic model
为验证 MCNN-CTC 以及 SE-MCNN-CTC 声
声学模型 建模单元 参数数量 测试集错误率/% 学 模 型 的 泛 化 能 力， 选 取 Thchs30 数 据
MCNN(7)-CTC 音节 4.77 M 23.43 集 中 DCNN(7)-CTC、 MCNN(7)-CTC 以 及 SE-
MCNN(8)-CTC 音节 3.61 M 24.85
MCNN(7)-CTC 三个不同的声学模型在 ST-CMDS
MCNN(9)-CTC 音节 3.72 M 25.18
数据集上进一步实验。图 7(a) 和图 7(b) 分别表示
SE-MCNN(7)-CTC 音节 4.82 M 23.05
声学模型训练与微调的损失值变化曲线。可以看