Page 54 - 《应用声学》2020年第3期

374 2020 年 5 月

ᣣ࠱᭧ ԍႃᬝၬಏ ᣣ࠱᭧

᣿૱ᑟ٨˗ॷ੕᭧ڏ ᣿૱ᑟ٨˗ॷ੕᭧ڏ
ဗතಞᑠ

R R 2
R 1 1
r r 1 1
r 2
r 2
H H 2 2
H 1
h
h 1 h 1 h 2 2
d 1 d 2
(a) ˗ᫎᘙː᣸Ԓ (b) ˗ᫎԒː᣸ᘙ

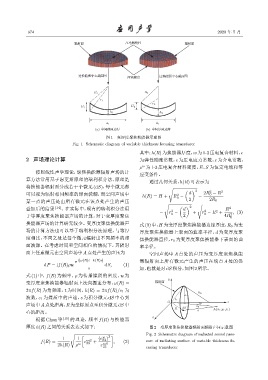
图 1 变厚度聚焦换能器示意图
Fig. 1 Schematic diagram of variable thickness focusing transducer

其中：h(R) 为换能器厚度，w 为1-3 压电复合材料，c
2 声场理论计算 为弹性刚度常数，e 为压电应力常数，ε 为介电常数，

w
ρ 为 1-3 压电复合材料密度，E、S 为恒定电场和等
按照线性声学理论，聚焦换能器辐射声场的计
应变条件。
算方法常用基于惠更斯原理的瑞利积分法，原理是
通过几何关系，h(R)可表示为
将换能器辐射面分成若干个微元 (dS)，每个微元都 √
( ) 2 2 2
可以视为辐射相同频率的球面波源，而空间声场中 2 d 2R − R
0
h(R) = H +
R −
0 −
某一点的声压是由所有微元在该点处产生的声压 2 2R 0
√ √
叠加后的结果 [14] 。在实际中，现有的瑞利积分法用 ( ) 2 R 4
d
2
2
2
− r − + r − R + , (3)
0
0
于等厚度聚焦换能器声场的计算，对于变厚度聚焦 2 4R 0 2
换能器声场的计算研究较少。变厚度聚焦换能器声 式(3)中，H 为变厚度聚焦换能器边缘厚度，R 0 为变
场的计算方法也可以基于瑞利积分法原理，与等厚 厚度聚焦换能器上表面的曲率半径，d 为变厚度聚
度相比，不同之处是每个微元辐射出不同频率的球 焦换能器直径，r 0 为变厚度聚焦换能器下表面的曲
面波源。在考虑时间和空间相位的情况下，其辐射 率半径。
面上任意微元在空间声场中A点处产生的声压为 空间声场中 A 点处的声压为变厚度聚焦换能
e i[ω(R)t−k(R)s] 器辐射面上所有微元产生的声压在场点 A 处的叠
dP = if(R)ρu dS, (1)
s 加，也就是对dS 积分，如图2所示。
式 (1) 中，f(R) 为频率，ρ 为传播媒质的密度，u 为
y
变厚度聚焦换能器辐射面上法向振速分布，ω(R) = ᣣ࠱᭧
2πf(R) 为角频率，t 为时间，k(R) = 2πf(R)/c 1 为
R 0
a
波数，c 1 为媒质中的声速，s 为积分微元 dS 中心到 b
O z
声场中A点处距离，R 为坐标原点至积分微元dS 中 θ
R dS s  A↼x  ֒y  ֒z  ↽
心的距离。 s
根据 Chan 等 [15] 的理论，频率 f(R) 与换能器 x
厚度h(R)之间的关系表达式如下： 图 2 变厚度聚焦换能器辐射面辐射声压示意图
√ Fig. 2 Schematic diagram of radiated sound pres-
[ w 2 ]
1 1 (e )
33
f(R) = c wE + , (2) sure of radiating surface of variable thickness fo-
33
2h(R) ρ w ε wS
33 cusing transducer