Page 86 - 《应用声学》2020年第3期

406 2020 年 5 月

∫ T
1 |∇p i (t)| = 1，此时的相关函数曲线仅与噪声信号
R AP = lim |A(t) − ¯a(t)|
T →∞ 2T 相关，记相关函数值为 R(∆t) ；图 7(b) 为公式 (5)
1
−T
· |∇(P(t) − ¯p(t))| · dt, (3) 中设噪声信号值等于 1，即取 |a i (t)| = 1，此时的
相关函数曲线仅与压力梯度相关，记相关函数值为
式 (3) 中，R AP (t) 为波动信号的相关函数。将公
R(∆t) 。
2
式 (1)和公式(2)代入到公式(3)得
∫ T 1.0
1
R AP = lim |a(t)| · |∇p(t)| · dt. (4) 0.5
T →∞ 2T −T ᄱࠫܦू 0
上述是针对两列无限长的、连续信号之间的相 -0.5
关性考察，而在实际的测量或应用中，由传感器测量 -1.0 0
的信号通常为离散信号。考虑在时间间隔 ∆t 内的
离散信号，采样频率为 f s ，N 表示在 ∆t 时间间隔内 ᄱࠫԍҧ/kPa -10 ࣰ੸
的采集点数，即采样数。上述公式可转化为 -20 ൤࣢෺໤ ࣰ੸1 ࣰ੸2 3
0 1 2 3 4 5 6 7 8 9 10 11 12
N
1 ∑ ௑ᫎ/s
R AP (∆t) = |a i (t)| · |∇p i (t)|,
N
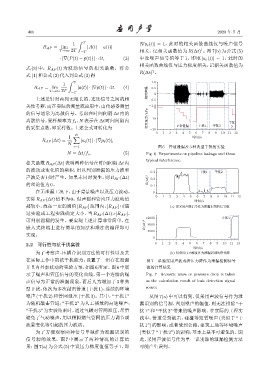
i=1 图 6 管道泄漏及 3 种典型干扰的实验
N = ∆t/f s . (5) Fig. 6 Experiments on pipeline leakage and three
typical interference
相关函数 R AP (∆t) 表明两种信号在时间间隔 ∆t 内
的波动或变化值的乘积，用以判别泄漏的压力波和
0.3 ࣰ੸1 ࣰ੸2
声波是否同时产生。如果未同时发生，则 R AP (∆t) R↼∆t↽  0.2
的理论值为0。 0.1
在无泄漏工况下，由于背景噪声以及压力波动， 0
实际 R AP (∆t) 值不为 0。但声强和管内压力波动值 0 1 2 3 4 5 6 7 8 9 10 11 12
௑ᫎ/s
都较小，故在一定的阈值 [R AP ] 范围内，[R AP ] 可通 (a) ̩᧔ၹܦฉηՂͻ˞෺໤គѿᄊηՂູ
过实验或工程实践确定大小，当 R AP (∆t)>[R AP ]，
12000 ࣰ੸3
可判别泄漏的发生。要实现上述计算非常简单，在
嵌入式终端上进行简单的加法和乘法的编程即可 R↼∆t↽  8000
4000
实现。
0
2.2 可行性与抗干扰实验 0 1 2 3 4 5 6 7 8 9 10 11 12
௑ᫎ/s
为了考察声 -压耦合识别方法的可行性以及其 (b) ̩᧔ၹԍҧ೙एͻ˞෺໤គѿᄊηՂູ
在实际工作中的抗干扰能力，设置了一组存在泄漏 图 7 单独采用声波或者压力降作为泄漏检测信号
并且有外加扰动的实验方案，如图6所示。图6 中展 源的计算结果
示了噪声和管压信号的变化曲线，第一个连续的噪 Fig. 7 Acoustic wave or pressure drop is taken
声信号为正常的泄漏现象，而后人为增加了 3 种典 as the calculation result of leak detection signal
型干扰，依次为多次敲击管道 (干扰 1)、连续的环境 source
噪声 (干扰 2) 和管网泄压 (干扰 3)。其中，“干扰 1” 从图 7(a) 中可以看到，仅采用声波信号作为泄
为随机敲击管道；“干扰 2” 为人工播放的高速噪声； 漏识别的信号源，判别噪声的幅值，则无法排除 “干
“干扰 3” 为实验结束时，通过气罐对管网泄压，尽量 扰1”和“干扰2”带来的噪声影响。在实际的工程实
避免了气动噪声，用以模拟燃气管网的压力调节或 践中，管道受到敲击、碰撞等短暂噪声 (类似于 “干
流量变化等引起的压力波动。 扰1”) 的影响，或者受到公路、建筑工地等环境噪声
为了方便观察两种信号单独作为泄漏识别的 (类似于“干扰2”)的影响，基本上是不可避免的。因
信号源的效果，图 7 中展示了两种情况的计算结 此，采用声波信号作为单一识别源的泄漏检测方法
果：图 7(a) 为公式 (5) 中设压力梯度值恒等于 1，即 可能产生误判。