Page 155 - 《应用声学》2020年第4期

第 39 卷 第 4 期 陆昕等： 干式变压器有限元仿真模型的电磁和振动分析 641

压器内部电磁力计算的理论还不能给出完全精确 物体实际的振动是各阶振动的结合，但是高阶
的计算结果。因此，为了使问题简化，在输入给定激 振动相对来说影响较小，因此主要考察前 6 阶的振
励的条件下，以数值模拟的方法来计算相对振动的 动特性即可。从图 5 中也不难发现，频率在 1000 Hz
幅值。 以内时是振动集中的主要位置。前 6 阶模态对应的
云图中典型部分如图6所示。
3 干式变压器仿真振动分析 在图 6 中，干式变压器的每种模态代表的是变

压器的振动形式。从图 6 可以看出，铁芯顶部及夹
3.1 模态分析
件与绕组的振动相对于干式变压器本体的其他位
模态分析是以响应频谱分析为基础的计算结
置来说更为强烈，所以在考虑本体的谐响应分析时，
构振动特性的数值技术，结构振动特性包括振型以
只需主要考察铁芯、绕组线圈、变压器上端夹件等
及固有频率 [15] 。针对本文中对应的变压器本体模
几个位置的振动情况。
型，求取的前100阶模态的固有频率，如图5所示。
3.2 谐响应分析

1500 由于干式变压器的结构比油浸式变压器简单，
若不考虑底部风机的振动，变压器的噪声则主要由
ᮠဋ/Hz 1000 铁芯和绕组线圈的振动引起。在进行谐响应分析时，
将等效的振动力施加在铁芯和线圈的上沿，根据实
测值输入，再考察线圈位置、风扇位置、铁芯顶部、上
500
端排线、左侧铁芯的响应，进行对照。显然，各个单
元之间的响应特性并不完全一致，此时只要比较最
0
0 20 40 60 80 100 大的振动幅值即可。输入的数据可以根据实际测量
വগ᫽஝
的结果得到，如图7所示。
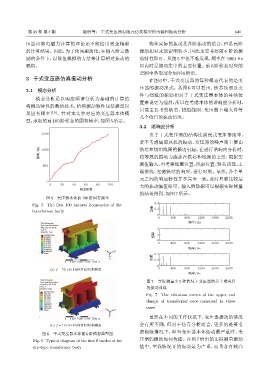
图 5 变压器本体前 100 阶固有频率
Fig. 5 The first 100 natural frequencies of the 0.4
transformer body ቇᣒ 0.2
0
0 400 800 1200 1600 2000
ᮠဋ/Hz
Tatal deformation
Type: taotal deformation
Frequency: 76.126 Hz 2
Unit: m
2016/1/21 13:44
0.030373 Max ᆁ᡹ 1
0.026998
0.023623 0
0.020249
0.016874 0 400 800 1200 1600 2000
0.013499
0.010124 ᮠဋ/Hz
0.0067495
0.0033748 x y
0 Min 0.4
᠇ᣒ
z 0.2
0 0.250 0.500 0.750 1.000 m
0
(a) f=76.126 Hz௑ࠫऄᄊ2᫽വগ 0 400 800 1200 1600 2000
ᮠဋ/Hz
Tatal deformation 实际测量中 3 种情况下变压器铁芯上端夹件
Type: taotal deformation 图 7
Frequency: 161.35 Hz
Unit: m 的振动曲线
2016/1/21 13:44
0.024013 Max
0.021345 Fig. 7 The vibration curves of the upper end
0.018677
0.016009
0.013341 clamps of transformer core measured in three
0.010672
0.0080044
0.0053362
0.0026681 x y cases
0 Min
z 虽然在不同的工作状况下，变压器振动的情况
0 0.250 0.500 0.750 1.000 m
(b) f=110.83 Hz௑ࠫऄᄊ5᫽വগ 会有所不同，但对于仿真分析而言，更多的是要考
虑极限情况下，即当变压器本体振动最严重时，变
图 6 干式变压器本体前 6 阶模态典型图
Fig. 6 Typical diagram of the first 6 modes of the 压器的振动如何传播。在图 7 给出的实际测量振动
dry-type transformer body 值中，空载情况下的振动最为严重，而且含有较高