Page 150 - 《应用声学》2020年第4期
P. 150
636 2020 年 7 月
图 4 结果表明 “DGD-FxLMS” 算法在最大降 “DGD-FxLMS” 算法会在两个梯度方向上进行切
噪量上比 “FxLMS” 算法和 “Rescaling” 算法差,从 换,但并不会在收敛过程中出现系统不稳定性问题。
式 (3) 可以看出 “FxLMS” 算法在搜索最佳权矢量
0
过程中没有考虑其他任何约束条件,而仅仅以将误 FxLMS
Leaky
差信号能量降到最低为目标,因此它虽然最大降噪 Rescaling
DGD-FxLMS
量高,噪声放大也最大。 -5
“Rescaling” 算法效果较好,既有不错的降噪
量,噪声放大也不大,但从式 (11) 和式 (12) 来看,在 ൷ᯩ䈟ᐞ/dB
实际的数字信号处理器件应用中,除法运算会消耗 -10
较大资源,此外,该算法是采用 “硬性” 削波的方式
对次级信号进行处理,没有明确的代价函数。
-15
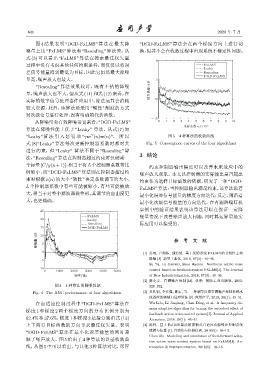
从降噪量和有效降噪带宽来看,“DGD-FxLMS” 0 1 2 3 4 5 6 7 8 9 10
䟷ṧ⛩ᮠ n/T10 5
算法在降噪性能上优于 “Leaky” 算法。从式 (7) 知
T
“Leaky” 算 法 引 入 惩 罚 项 “γw (n)w(n)”, 所 以 图 5 4 种算法的收敛曲线
式 (8)“Leaky” 算法每次更新控制器系数时都对其 Fig. 5 Convergence curves of the four algorithms
进行约束,但 “Leaky” 算法不同于 “Rescaling” 算
3 结论
法,“Rescaling” 算法在控制器超过约束时仅硬乘一
个标量[C/y(n + 1)],相当于将L个控制器系数等比
约束控制器输出幅度可以改善水床效应中的
例缩小,而 “DGD-FxLMS” 算法则在控制器超过约 噪声放大现象。本文以控制器的实际输出是否超出
束时根据 x(n) 的大小 “软性” 决定系数调节的大小,
约束作为选择目标函数的依据,研究了一种“DGD-
L 个控制器系数中有些可能被缩小,有些可能被放
FxLMS”算法:当控制器输出满足约束,该算法沿着
大,相当于对整个滤波器做整形,其调节的自由度更 最小化误差信号能量的梯度方向迭代;反之,则沿着
大,也更精确。 最小化次级信号能量的方向迭代。在有源降噪耳机
实例中的验证结果表明该算法可以在保证一定降
25
FxLMS 噪量情况下改善噪声放大问题,同时其运算量是实
20 Leaky
Rescaling 际应用可以接受的。
15 DGD-FxLMS
ᬌ٪᧚/dB 10 5 参 考 文 献
0 [1] 苏雨, 卢剑伟, 邵浩然. 基于反馈系统 FXLMS 的非线性主动
降噪 [J]. 新型工业化, 2018, 87(3): 40–46.
-5
Su Yu, Lu Jianwei, Shao Haoran. Nonlinear active noise
-10
0 1000 2000 3000 4000 5000 control based on feedback system FXLMS[J]. The Journal
ᮠဋ/Hz of New Industrialization, 2018, 87(3): 40–46.
[2] 陈克安. 有源噪声控制 [M]. 北京: 国防工业出版社, 2003:
图 4 4 种算法的降噪性能 328–332.
Fig. 4 The ANC performance of four algorithms [3] 吴礼福, 李佳强, 陈定, 等. 一种调节反馈有源噪声控制系统水
床效应的频域自适应算法 [J]. 应用声学, 2019, 38(1): 45–51.
在自适应控制过程中 “DGD-FxLMS” 算法在 Wu Lifu, Li Jiaqiang, Chen Ding, et al. A frequency do-
main adaptive algorithm for tuning the waterbed effect of
梯度 1 和梯度 2 两个梯度方向的分布比例分别为
feedback active noise control system[J]. Journal of Applied
62.4% 和 37.6%,梯度 1 和梯度 2 是指分别沿式 (13) Acoustics, 2019, 38(1): 45–51.
上下两行目标函数的方向寻求最佳权矢量。表明 [4] 陈智. 基于 FxLMS 算法的前馈式自适应有源噪声控制系统
“DGD-FxLMS” 算法在最小化误差能量的同时兼 建模与仿真 [J]. 自动化与仪器仪表, 2018(5): 10–13.
Chen Zhi. Modeling and simulation of feed-forward adap-
顾了噪声放大。图 5 给出了 4 种算法的误差收敛曲
tive active noise control system based on FxLMS[J]. Au-
线,从图 5 中可以看出,与其他 3 种算法对比,尽管 tomation & Instrumentation, 2018(5): 10–13.