Page 136 - 《应用声学》2021年第2期

304 2021 年 3 月

0 引言 ඵ۫

圆管换能器由于其结构简单、性能可靠、声辐 Ѹভ᣸ႍ
射面积大、辐射效率高等优点，在水声及超声领域
ړኮ૱ᑟ٨
有广泛应用。Morse [1] 最早研究圆柱体声辐射问题，
基于柱坐标系下的声波方程给出了圆柱体辐射声 Ѹভ᣸ႍ
场和格林函数的表达式。Junger 研究了速度在轴
向均匀分布以及在轴向和周向周期性变化的无限
长圆柱的辐射阻抗 [2] ，并推导了简谐力作用下无
限长弹性壳体表面的位移和流体中的声压分布 [3] 。 图 1 圆管换能器有限元模型
Robey [4] 基于格林函数推导了圆管均匀振动的自 Fig. 1 Finite element model of a cylindrical transducer
辐射和相互辐射阻，并讨论了圆管之间的距离对辐
1.2
射阻的影响。Greenspon 等 [5] 研究了无限长刚性圆
柱体上矩形活塞的声压和互辐射阻抗，并对平面、 1.0
球体和圆柱体上的活塞的互辐射阻抗进行了比较。 0.8 h⊳r/⊲
Sandman [6] 研究了两端有刚性固定端面支撑的有 ॆʷӑᣣ࠱᫾ 0.6 h⊳r/⊲
h⊳r/⊲
限长圆柱壳体的辐射阻抗，在计算有限长圆柱壳流
0.4
体负载时，可以用无限长刚性障柱上的圆柱壳体模
型来近似。Steppanishen [7] 研究了引入壳理论的弹 0.2
性圆柱壳辐射阻抗的渐进表达式，并讨论了不同振 0
0 1 2 3 4 5 6 7 8 9 10
动模式对声辐射的相互耦合效应。Bulter等 [8] 建立 kr

了刚性扩展模型，利用傅里叶级数法计算了0 ∼ 2阶 图 2 有限元计算辐射阻
圆管圆周模态的辐射阻抗。当圆管高径比 h/r > 2 Fig. 2 Finite element calculation results of radi-
时，利用刚性扩展模型可以较好地表述圆管换能器 ation resistance
的辐射阻抗，但随着高径比 (h/r) 的减小，模型计算
0.7
的辐射阻抗与实际存在较大误差，因此，有必要对短 h⊳r/⊲
0.6 h⊳r/⊲
圆管情况下 (1 6 h/r 6 2) 的辐射阻抗进行更精确 h⊳r/⊲
0.5
的估计。
ॆʷӑᣣ࠱ઈ 0.4

1 圆管换能器有限元分析 0.3
0.2
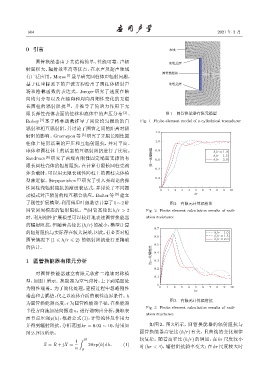
对圆管换能器建立有限元软件二维轴对称模
0.1
型，如图 1 所示。换能器为空气背衬，上下两端面处
0
为刚性端盖。为了简化处理，建模过程中忽略刚性 0 1 2 3 4 5 6 7 8 9 10
kr
端盖和去耦垫，代之以流体介质的刚性边界条件。h
图 3 有限元计算辐射抗
为圆管换能器高度，r 为圆管换能器半径，在换能器
Fig. 3 Finite element calculation results of radi-
半径方向施加法向振速u。进行谐响应分析，提取表
ation reactance
面节点压强 p(h)，根据公式 (1)，计算流体反作用力
并得到辐射阻抗，分析范围kr = 0.03 ∼ 10，结果如 如图 2、图 3 所示，圆管换能器的辐射阻抗与

图2、图3所示。 圆管换能器高径比 (h/r) 有关，且曲线的变化规律
∫ H 较复杂。随着高径比 (h/r) 的增加，在 kr 尺度较小
1
Z = R + jX = 2πrp(h)dh. (1) 时 (kr < 4)，辐射阻抗斜率变大；在 kr 尺度较大时
u 0