Page 137 - 《应用声学》2021年第2期

第 40 卷 第 2 期 梁家宁等： 短圆管换能器辐射阻抗 305

(kr > 4)，辐射阻抗波动起伏减小。 3 辐射阻抗经验公式模型有效性验证

2 圆管换能器辐射阻抗的曲线拟合 为了估计圆管换能器辐射阻抗，Bulter 提出了
圆管刚性扩展模型。声场的瑞利积分可近似考虑成
由于圆管声场瑞利积分求解的复杂性，想直 傅里叶级数的叠加，得到的辐射阻抗公式为 [8]
接得到圆管换能器辐射阻抗的解析解是很困难 ∑ ( khm )
∞
2
的 [9−10] 。因此，提出一种圆管辐射阻抗经验公式的 Z = 2iπrh ρω ε m sinc 2 2M
m=0
表达形式。为了确定经验公式的母函数形式，仔细
H 0 (β m r)
研究图 2、图 3 中曲线，发现其具有以下特点：(1) 辐 × ′ , (4)
β m dH (β m r)
0
射阻抗受两因素影响，分别是圆管的高径比 (h/r) 2 1/2 ，M = d/λ，d为间距。
其中，β m = k[1 − (m/M) ]
和波数k。因此，母函数中应带有两自变量；(2) 曲线 下面，选取高径比 h/r = 1、h/r = 1.5、h/r = 2
存在渐进特性，辐射阻的渐进值 R ∞ = ρcS，辐射抗 三组数据对比分析经验公式与刚性扩展模型计算
的渐进值 X ∞ = 0；(3) 曲线存在振荡特性，且振荡 辐射阻抗结果。
幅度呈衰减规律；(4) 曲线在 kr 较小时的增长趋势 由图 4∼ 图 9 对比可以看出，在 1 6 h/r 6 2 的

类似于脉动球源的辐射阻抗曲线。 范围内，经验公式计算得到的辐射阻抗与有限元结
根据以上特点，选择处理方法和函数类型：(1) 果较为相符，拟合程度较高。随后计算曲线拟合、傅
设经验公式的两自变量为 kh、 kr； (2) 渐进特性：将 里叶级数解与有限元计算得到的辐射阻抗的拟合
参量减去渐进值，作为新变量参与曲线拟合；(3) 振
1.2
荡特性及衰减规律：用 sinc 函数进行拟合；(4) 设定
1.0
母函数时参考脉动球源辐射阻抗公式。
选取在 1 6 h/r 6 2 范围内 500 组等间隔经有 0.8
限元计算得到的数值解，在 MATLAB 中进行曲线 ॆʷӑᣣ࠱᫾ 0.6
拟合。根据以上原则，经过反复逼近拟合，得到辐 0.4
射阻抗拟合后的数学表达式，如公式 (2)、公式 (3) 0.2 దᬍЋᝠካ
జጳલՌ
Ϭ᧗Ձጟ஝ᝍ
所示。 0
(1) 归一化辐射阻经验公式为 -0.2
0 2 4 6 8 10 12
R [ 64 ] kr
= 1−175 exp − 3(0.011kh+0.012kr) +0.93
ρcS
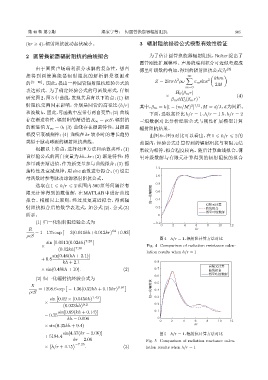
图 4 h/r = 1，辐射阻计算方法对比
[ 7.28 ]
sin 0.0013(0.02kh)
× Fig. 4 Comparison of radiation resistance calcu-
(0.02kh) 7.35
lation results when h/r = 1
sin[0.46(kh + 2.1)]
+ 0.8
kh + 2.1 0.8
దᬍЋᝠካ
× sin(0.48kh + 10). (2) 0.7 జጳલՌ
Ϭ᧗Ձጟ஝ᝍ
0.6
(2) 归一化辐射抗经验公式为
X [ 0.61 ] 0.5
= 1208.6 exp − 1.36(0.52kh + 0.15kr) ᖂаॆ䗀ሴᣇ 0.4
ρcS
[ 1.43 ] 0.3
sin 0.02 × (0.045kh)
× 0.2
(0.023kh) 0.2
sin[0.69(kh + 0.14)] 0.1
− 0.75
kh − 0.006 0
0 2 4 6 8 10 12
× sin(0.35kh + 9.4) kr
sin[4.37(kr − 2.06)] 图 5 h/r = 1，辐射抗计算方法对比
+ 5184.4
kr − 2.06 Fig. 5 Comparison of radiation reactance calcu-
( ) −7.25
× h/r + 4.15 . (3) lation results when h/r = 1