Page 142 - 《应用声学》2021年第2期

310 2021 年 3 月

慢均匀变化，幅度维持在一定范围内，具有局部平稳 算子 (F oc )、闭 -开算子 (F co )、开闭 -闭开组合算子
特性。 (Combination morphological filter, CMF)、高帽算
混响可以看作是一种因主动发射信号引起的 子(Top-hot filtering, THF)等，其定义分别为
有色干扰噪声，其频域上覆盖的区域与发射信号基
F oc (f) = f ◦ b • b, (7)
本重合，时域上与发射信号及目标回波强相关。在
F co (f) = f • b ◦ b, (8)
声呐探测画面中，会在主动探测历程图中产生大面
积的强干扰，影响距离范围广。从混响的时空特性 CMF(f) = (F co (f) + F oc (f))/2, (9)
上看，混响是时、空变的，其强度随时间增加一般逐 THF(f) = f − f ◦ b. (10)
渐衰减，是非平稳的。 准确描述形态滤波器的频率响应特性是其应
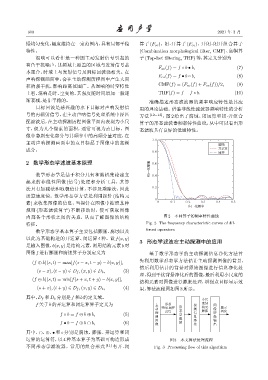
目标回波是感兴趣的水下目标对声呐发射信 用的理论基础。借鉴非线性滤波器频响特性的分析
号的再辐射信号，在主动声呐信号处理系统中经匹 方法 [12−13] ，图 2 给出了腐蚀、闭运算和闭 -开组合
配滤波后，在主动探测历程图像平面内表现为小尺 算子的形态滤波器频率特性曲线，从中可以看出形
寸，仅为几个像素的面积，通常可视为点目标。图 态滤波具有良好的低通特性。
像中急剧变化部分与其频率中的高频分量对应，在
1.0
主动声呐探测画面中的点目标属于图像中的高频 ᑼᙍ
成分。 0.8 नᤂካ
᫇न
2 数学形态学滤波基本原理 0.6

数学形态学是基于积分几何和随机集论建立 ॆʷӑࣨϙ 0.4
起来的非线性图像 (信号) 处理和分析工具，其算
法只有加减法和取极值计算，不涉及乘除法，因此 0.2
运算速度快。数学形态学方法是利用探针 (结构元
0
素) 来收集图像的信息，当探针在图像中按照某种 0 0.1 0.2 0.3 0.4 0.5
ॆʷӑᮠဋ
规则 (形态滤波算子) 不断移动时，便可获取图像
内部各个形状之间的关系，从而了解图像的结构 图 2 不同算子的频率特性曲线
特征。 Fig. 2 The frequency characteristic curves of dif-
数学形态学基本算子主要包括膨胀、腐蚀以及 ferent operators

以此为基础构造的开运算、闭运算 4 种。设 f(x, y) 3 形态学滤波在主动探测中的应用
是输入图像，b(x, y) 是结构元素，则用结构元素 b 对
图像f 进行膨胀和腐蚀算子分别定义为 基于数学形态学的主动探测信息净化方法首

先利用数学形态学方法估计主动探测图像的背景，
(f ⊕ b)(s, t) = max[f(s − x, t − y) − b(x, y)],
然后利用估计的背景对原始图像进行信息净化处
(s − x), (t − y) ∈ D f , (x, y) ∈ D b , (3)
理，得到干扰背景净化后的图像，最后利用小尺度的
(f ⊖ b)(s, t) = min[f(s + x, t + y) − b(x, y)],
结构元素对图像进行膨胀处理，增强点目标显示效
(s + x), (t + y) ∈ D f , (x, y) ∈ D b , (4) 果，算法流程图如图3所示。

其中，D f 和D b 分别是f 和b的定义域。 ࠵ࡇ
f 关于b的开运算和闭运算算子定义为 ˟ ॎগ ଊ एፇ ڏ
ү न᫇-᫇न ॎ ฾ ౞Ћ ϸ ௭ᇨ
গ
ᒟᐺ
Ѽх
ᤂካ
f ◦ b = f ⊖ b ⊕ b, (5) ଊ ߦ η ܙ
฾ ৌ ू
ڏ ໚ ь ᣥ
f • b = f ⊕ b ⊖ b, (6) ϸ ฉ ӑ ѣ
其中，⊖、⊕、• 和 ◦ 分别是腐蚀、膨胀、开运算和闭
运算的运算符，以 4 种基本算子为基础可构造形成 图 3 本文算法处理流程
不同形态学滤波器。常用的组合形式 [11] 有开 -闭 Fig. 3 Processing flow of this algorithm