Page 143 - 《应用声学》2021年第2期

第 40 卷 第 2 期 王功兵等： 基于数学形态学的主动声呐探测信息净化方法 311

3.1 结构元素确定 下的频率特性曲线，结果如图 5 所示，可以看出，L
由 1.2 节分析可知，主动探测画面中的干扰主 越大通带的宽度越窄。进一步计算开闭 -闭开组合
要是被动条状干扰以及大面积团状混响干扰，是主 算子在不同长度L下的截止频率，如表1所示。
动探测图像的主要干扰背景，是声呐探测中不感兴
1.0
趣的部分，图像净化就是将这部分滤除。根据干扰
L/
背景特性，结构元素的选择类型较多，如线形、方形、 L/
0.8 L/
球形等。 L/
而感兴趣的水下目标回波一般为小尺寸的，在 0.6
图像中只占几个像素点的点状目标。为了保留图像 ॆʷӑࣨϙ
中点状目标，本文选择竖线型结构元，并且竖线型与 0.4
图像背景干扰 (条状干扰及团状混响) 较为吻合，可
以更好地估计背景。 0.2
图4 是某一主动方位历程图中目标所在波束部
0
分数据，其中有一凸起尖峰，表示目标回波，其余部 0 0.1 0.2 0.3 0.4 0.5
ॆʷӑᮠဋ
分为背景噪声。从图4中可以看出，由于开运算的收
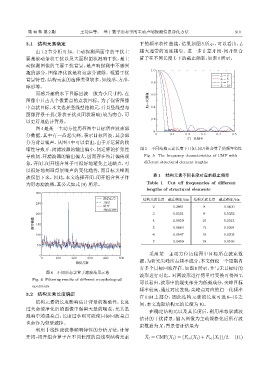
缩性导致开-闭滤波器的输出偏小，闭运算的扩张性 图 5 不同结构元素长度下开闭 -闭开组合算子的频率特性
导致闭-开滤波器的输出偏大，因而存在统计偏倚现 Fig. 5 The frequency characteristics of CMF with
象，开闭 -闭开组合算子可很好地避免上述缺点，可 different structural element lengths
以很好地刻画背景噪声的变化趋势，而目标尖峰则
表 1 结构元素不同长度对应的截止频率
被保留下来。因此，本文选择开闭 -闭开组合算子作
为形态滤波器，其公式如式(9) 所示。 Table 1 Cut off frequencies of different
lengths of structural elements
300
ԔݽηՂ 结构元素长度 截止频率/Hz 结构元素长度 截止频率/Hz
250 न᫇
᫇न 2 0.2051 8 0.0400
न᫇-᫇न
200 3 0.1201 9 0.0352
ᄱࠫࣨϙ 150 4 0.0859 10 0.0313
0.0664
12
5
0.0264
100 6 0.0547 15 0.0205
7 0.0459 18 0.0166
50
采用某一主动方位历程图中目标所在波束数
0
0 100 200 300 400 500
஝૶ག஝ 据，为研究尖峰所占频率成分，本文假设一个周期内
有多个目标回波存在，如图 6所示，并与无目标时的
图 4 不同形态学算子滤波结果示意
波形进行对比。对两波形进行傅里叶变换可得图 7，
Fig. 4 Filtering results of different morphological
可以看出，波形中的缓变部分为低频成分，尖峰目标
operators
频率较高，通过对比发现，尖峰点对应的归一化频率
3.2 结构元素长度确定
在 0.04 上部分，因此结构元素的长度可选 8∼15 之
结构元素的长度影响估计背景的准确性，长度
间，本文选取结构元的长度为10。
过大会使净化后的图像中保留大量的噪点，尤其是
在确定结构元以及其长度后，利用形态学滤波
混响中的强亮点；长度过小则可能使目标回波亮点
估计的干扰背景，输入图像为主动规格化后所有波
也会作为背景滤掉。
束数据为X，背景估计结果为
利用非线性滤波器频响特性的分析方法，计算
ˆ
开闭 -闭开组合算子在不同长度的直线型结构元素 X l = CMF(X l ) = (F co (X l ) + F oc (X l ))/2. (11)