Page 54 - 《应用声学》2021年第2期

222 2021 年 3 月

ܙԍ٨-ᣉՔவՔ ܙԍ٨ᤃڤ
20.0 20.0
17.5 17.5
15.0 15.0

f/kHz 12.5 f/kHz 12.5 6᫽٪ܦ
5᫽٪ܦ
10.0
10.0
7.5 7.5 4᫽٪ܦ
ܙԍ٨ʷ᫽૝ү
5.0 5.0
2.5 2.5

⊲⊲     ⊲⊲ ⊲    
t/s t/s
 ⊲ ⊲ ⊲ ⊲ ⊲         
a⊳g ܦԍጟ L/dB

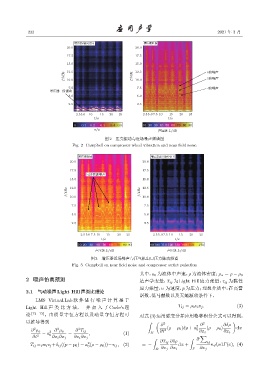
图 2 压壳振动与近场噪声频谱图
Fig. 2 Campbell on compressor wheel vibration and near field noise

ܙԍ٨ᤃڤ ܙԍ٨ѣ԰ᑢфηՂ
20.0 20.0

17.5 17.5
Տ൦ៈฉ٪ܦ
15.0 15.0

f/kHz 12.5 f/kHz 12.5
10.0
10.0
7.5 7.5

5.0 5.0
2.5 2.5

⊲⊲ ⊲     ⊲⊲ ⊲    
t/s t/s
                 
ܦԍጟ L/dB ܦԍጟ L/dB
图 3 增压器近场噪声与压气机出口压力脉动频谱
Fig. 3 Campbell on near field noise and compressor outlet pulsation

其中，a 0 为流体中声速，ρ 为流体密度；ρ a = ρ − ρ 0
2 噪声仿真预测 是声学变量，T ij 为 Light Hill 应力张量，τ ij 为黏性
应力张量，υ 为速度，p 为压力；理想介质中，在高雷
2.1 气动噪声Light Hill声类比理论
诺数、低马赫数以及无熵源项条件下，
LMS Virtual.Lab 软 件 进 行 噪 声 计 算 基 于
Light Hill 声 类 比 方 法， 并 加 入 了 Curle’s 理 T ij = ρ 0 v i v j . (3)
论 [12−13] 。由质量守恒方程以及动量守恒方程可 对式(3)运用强变分并应用格林积分公式可以得到：
以推导得到 ∫ ( ∂ 2 ∂ 2 ∂δρ )

2 2 2 (ρ − ρ 0 )δρ + a 2 0 (ρ − ρ 0 ) dx
∂ ρ a 2 ∂ ρ a ∂ T ij ∂t 2 ∂x i ∂x i
− a 0 = , (1) Ω
∂t 2 ∂x i ∂x j ∂x i ∂x j ∑
∫ ∂T ij ∂δρ ∫ ∂
2
T ij =ρv i v j +δ ij ((p − p 0 ) − a (ρ − ρ 0 ))−τ ij , (2) = − dx + ij n i δρdΓ(x), (4)
0
Ω ∂x j ∂x i Γ ∂x j