Page 68 - 《应用声学》2021年第3期

386 2021 年 5 月

表 2 室温 25 C，模型中使用的材料属性 模式时谐波大小分布。图 5 为声轴方向各谐波幅值
◦
Table 2 The material properties used in 大小分布。
the model when the Room temperature is MPa MPa
25 C -100 ⊲ -100 ⊲
◦
x/mm ⊲ x/mm ⊲
⊲
密度/ 声速/ 比热容/ 导热系数/ 0 0
◦ −1
(kg·m −3 ) (m·s −1 ) (J·kg −1 · C ) (W·m −1 ·K −1 ) ⊲ ⊲
⊲
水 1000 1483 4178 0.60 100 100
-100 0 100 -100 0 100
肝脏 1060 1568 3639 0.51 y/mm y/mm
脂肪 915 1468 2348 0.21 (a) ۳ฉ (b) ̄൓ៈฉ
MPa MPa
表 3 换能器参数 -100 ⊲ -100
⊲
Table 3 Transducer parameters ⊲
x/mm 0 ⊲ x/mm 0 ⊲
开口直径 孔直径 曲率半径 频率 ⊲ ⊲
d 1 /mm d 2 /mm r/mm f/MHz 100 100
-100 0 100 -100 0 100
200 80 165 1
y/mm y/mm
(c) ʼ൓ៈฉ (d) پ൓ៈฉ
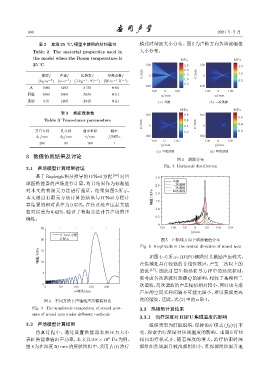
3 数值仿真结果及讨论
图 4 谐波分布
Fig. 4 Harmonic distribution
3.1 声场模型计算结果验证
基于 Rayleigh 积分推导的 O’Neil 方程 [16] 对凹 3.0
球面换能器的声场进行计算，将其结果作为标准值 ۳ฉ
2.5 ̄൓ៈฉ
ʼ൓ៈฉ
对本文的有限元方法进行验证。结果如图 3 所示， 2.0 پ൓ៈฉ
本文通过有限元方法计算的结果与 O’Neil 方程计 ࣨϙ/MPa
算结果的相对误差为 0.55%，在焦点处声压最大值 1.5
1.0
相对误差为 0.42%，验证了有限元法计算声场的正
确性。 0.5
0
25 -150 -100 -50 0 50 100 150
y/mm
OýNeilவሮ
20 దᬍЋ 图 5 声轴线方向上谐波幅值分布
Fig. 5 Amplitude in the central direction of sound axis
ࣨϙ/MPa 如图4∼5所示，HUFU辐照时其激励声压较大，
15
10
在焦域处具有较强的非线性效应，产生二次以上的
谐波 [17] ，因此计算生物热传导方程中的热沉积时，
5
需考虑各次谐波对热源 Q 的影响，相较于基频和二
0 次谐波，高次谐波的声压幅值相对较小，同时也考虑
0 50 100 150 200
ܦᣉጳ/mm 声压的空间采样间隔不可能无限小，难以获取更高

图 3 不同方法下声轴线声压幅值对比 次的谐波。因此，式(2)中的n取4。
Fig. 3 The amplitude comparison of sound pres- 3.3 热模型计算结果
sure of sound axis under different methods
3.3.1 治疗深度对HIFU焦域温度的影响
3.2 声场模型计算结果 组织类型为肝脏组织，保持治疗模式 (f 2 (t)) 不
仿真过程中，通过设置换能器表面压力大小 变，探索治疗深度对焦域温度的影响。由图 6 可知
表征换能器输出声功率，本文以 0.8 × 10 Pa 为例。 相同治疗模式下，随着深度的增大，治疗结束时深
6
图 4为在深度20 mm的肝脏组织中，采用f 1 (t)治疗 部组织焦域温升较浅部组织小，且深部组织温升速