Page 88 - 《应用声学》2021年第4期

572 2021 年 7 月

号稳定性的影响，在同一种工况下，以同一种网格划 0.040
0.032
分方式下，且压电片间距都为 0.6 m 时，用 10 kHz、 0.024
0.016
20 kHz、30 kHz、40 kHz 分别计算，导出接收端电 0.008
压信号，进行比较。如图 6 ∼ 9 所示，10 kHz 时，波 ଌஆቫႃԍ/V -0.008 0
形最为稳定，幅值波动不大，且无畸变现象；20 kHz -0.016
-0.024
-0.032
时，波形的幅值已经产生了一定的波动，但波形完 -0.040
 ⊲ ⊲ ⊲ ⊲
整，无畸变现象；但当频率增加到 30 kHz 和 40 kHz
௑ᫎ t/10 -4 s
时，波形已经非常不稳定，且幅值非常低。由此可
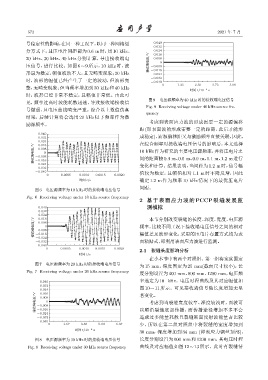
图 9 电压源频率为 40 kHz 时的接收端电压信号
见，频率过高时波能耗散迅速，导致接收端接收信
Fig. 9 Receiving voltage under 40 kHz source fre-
号微弱，且电压曲线畸变严重。综合以上数值仿真
quency
结果，后续计算将会选用 20 kHz 以下频率作为激
考虑到表面应力波的形成需要一定的源偏移
励源频率。
距 (即表面波的形成需要一定的距离，此后才能形
0.040
0.032 成稳定)，而源偏移距又与激励频率直接关联，因此，
0.024 在综合频率对接收端电压信号的影响后，本文选择
ଌஆቫႃԍ/V -0.008 10 kHz 作为研究的主要电压源频率，并将压电片之
0.016
0.008
0
间的距离按 0.4 m、0.6 m、0.9 m、1.1 m、1.2 m 进行
-0.016
-0.024 变化和计算。结果表明，当间距为 1.2 m 时，信号幅
-0.032
-0.040 值较为稳定，且幅值相对 1.1 m 时不降反增，因此
0 0.0005 0.0010 0.0015 0.0020
௑ᫎ t/s 确定 1.2 m 作为频率 10 kHz 情况下的最优压电片
间距。
图 6 电压源频率为 10 kHz 时的接收端电压信号
Fig. 6 Receiving voltage under 10 kHz source frequency
2 基于表面应力波的PCCP裂缝发展监
0.040 测模拟
0.032
0.024 本节分别改变裂缝的长度、深度、宽度、电压源
ଌஆቫႃԍ/V -0.008 0 频率，比较不同工况下接收端电压信号之间的相对
0.016
0.008
-0.016
-0.024 幅值差及波形变化，采用的压电片布置方式均为表
-0.032 面粘贴式，即利用表面应力波进行监测。
-0.040
0 0.0005 0.0010 0.0015 0.0020
2.1 裂缝长度影响分析
௑ᫎ t/s
在小本节中有两个对照组。第一组将宽度固定
图 7 电压源频率为 20 kHz 时的接收端电压信号
为 15 mm，深度固定为 25 mm(截面尺寸较小)，长
Fig. 7 Receiving voltage under 20 kHz source frequency
度分别设置为 400 mm、800 mm、1200 mm，电压频
率选定为 10 kHz。电压时程曲线及其对应幅值如
0.040
0.032
0.024 图 10 ∼ 11 所示。可见接收端信号随长度增加无显
ଌஆቫႃԍ/V -0.008 0 考虑到当裂缝宽度较窄、深度较浅时，面波可
0.016
著变化。
0.008
-0.016
-0.024 以顺沿裂缝底部传播，而传播途径增加不多不会
-0.032 造成过多能量耗散且裂缝断面反射波能量占比较
-0.040
 ⊲ ⊲ ⊲ ⊲ 少，所以在第二组对照组中将裂缝的宽度增加到
௑ᫎ t/10 -4 s
30 mm，深度增加到 34 mm (即预应力钢丝顶部)，
图 8 电压源频率为 30 kHz 时的接收端电压信号 长度分别设置为 600 mm 和 1200 mm，其电压时程
Fig. 8 Receiving voltage under 30 kHz source frequency 曲线及对应幅值如图 12 ∼ 13 所示。此时有裂缝情