Page 90 - 《应用声学》2021年第5期

734 2021 年 9 月

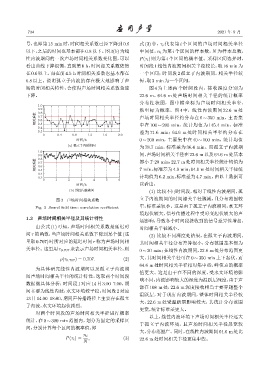
号，也即第15 min 时，时间相关系数已经下降到 0.6 式 (3) 中，τ i 代表第 i 个区间的声场时间相关半径
以下，之后的时间也基本都在0.8以下。图3(b)为线 中间值，n i 为第 i 个区间的样本数，N 为样本总数，
性内波期间的一次声场时间相关系数变化图，可以 P(τ i ) 则为第 i 个区间的概率值。采样区间选择时，
看出曲线下降很慢，直到第 6 h，时间相关系数依然 时间段 1 线性内波期间相关半径较长，取 16 min 为
在 0.6 以上，而在前 4.5 h 时间相关系数也基本都在 一个区间；时间段 2 孤立子内波期间，相关半径较
0.8 以上。说明孤立子内波的存在极大地影响了声 短，取3 min为一个区间。
场的时间相关特性，会使得声场时间相关系数急速 图 4 为上述两个时间段内，接收深度分别为
下降。 22.6 m、64.6 m 处声场时间相关半径的统计概率
分布柱状图，图中横坐标为声场时间相关半径，
1.0
0.9 纵坐标为概率。图 4 中，线性内波期间 22.6 m 处
0.8
ᄱТጇ஝ 0.7 声场时间相关半径约分布在 0 ∼ 350 min，主要集
0.6
0.5
0.4 中在 100 ∼ 200 min，统计均值为 145.4 min，标准
0.3 差为 71.6 min；64.6 m 处时间相关半径约分布在
0 0.4 0.8 1.2 1.6 2.0
௑ᫎ/h 0 ∼ 200 min，主要集中在 40 ∼ 100 min，统计均值
(a) ߤቡߕЯฉరᫎ
为 78.7 min，标准差为 36.4 min。而孤立子内波期
1.0
0.9 间，声场时间相关半径在22.6 m以及64.6 m处基本
0.8
ᄱТጇ஝ 0.7 都小于 20 min，22.7 m 处时间相关半径统计均值为
0.6
7 min，标准差为4.9 min；64.6 m处时间相关半径统
0.5
0.4
0.3 计均值为6.2 min，标准差为4.7 min。由以上数据可
0 1 2 3 4 5 6
以看出：
௑ᫎ/h
(b) ጳভЯฉరᫎ (1) 比较不同时间段，相对于线性内波期间，孤
图 3 声场时间相关系数 立子内波期间的时间相关半径骤减，且分布范围较
Fig. 3 Sound field time correlation coefficient 窄，标准差较小。这是由于孤立子内波期间，水文环
境起伏较大，信号传播过程中受时变起伏较大的声
1.3 声场时间相关半径及其统计特性
场影响，导致各个时间段接收到的信号差异性增加，
由公式 (1) 可知，声场时间相关系数是延迟时 时间相关半径减小。
间τ 的函数，当声场时间相关系数下降到某个值(这 (2) 比较不同深度处结果，在孤立子内波期间，
里取 0.707) 时所对应的延迟时间τ 称为声场时间相 其时间相关半径分布差异很小，分布范围基本都为
关半径。这里用τ 0.707 来表示声场时间相关半径，则 0 ∼ 20 min；在线性内波期间，22.6 m 处分布范围更

ρ(τ 0.707 ) = 0.707. (2) 大，其时间相关半径可在 0 ∼ 350 min 上下起伏，而
64.6 m 处时间相关半径相对集中些，峰值点的概率
为具体研究线性内波期间以及孤立子内波期
值更大。这是由于在不同的深度，受水文环境的影
间声场时间相关半径的统计特性，选取两个时间段
响不同，内波影响较大的深度为温跃层深度，由于声
数据做具体分析：时间段 1 对应 14 日 3:00–7:00，期
源在 108 m 处，22.6 m 深度接收相当于要穿越整个
间主要为线性内波，水文环境较平稳；时间段 2对应
温跃层，对于现行内波期间，整体时间相关半径较
13日14:00–18:00，期间声传播路径上主要存在孤立
大，22.6 m 处受温跃层影响较大，其统计分布范围
子内波，水文环境起伏剧烈。
更宽，统计标准差更大。
对两个时间段的声场时间相关半径进行概率
以上，线性内波环境下声场时间相关半径远大
统计，在 0 ∼ 300 min 范围内，划分为固定的采样区
于孤立子内波环境，且声场时间相关半径展宽较
间，分别计算每个区间的概率值，即
大，分布范围广。同时，在线性内波期间64.6 m处比
n i
P(τ i ) = , (3) 22.6 m处时间相关半径更集中些。
N