Page 96 - 《应用声学》2021年第5期

740 2021 年 9 月

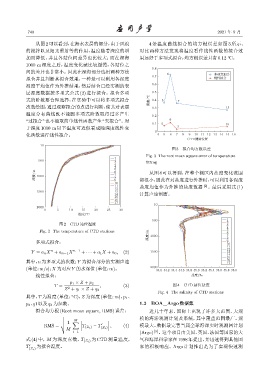
从图 2可以看到，在海水表层的部分，由于风浪 4 条温度曲线拟合的均方根误差如图 3 所示。
的搅拌以及阳光照射等的作用，温度随着深度的增 对比两种方法发现将温度看作线性函数的拟合效
加而降低，并且各站位间差异也比较大；而在深海 果远好于多项式拟合，均方根误差只有0.12 C。
◦
1000 m 深度之后，温度变化就比较缓慢，各站位之
0.8
间的差异也非常小。因此在深海部分选用两种方法 6
0.7 ܳᮊरલՌ
拟合并且判断其拟合效果，一种是可以利用各深度 ጳভલՌ
温度平均值作为外推结果，然后结合已经实测的表 0.6
层温度数据按多项式公式 (2) 进行拟合。拟合多项 0.5
式的阶数要合理选择，在实验中可以将多项式拟合 ឨࣀ/C 0.4 5 7
次数绘图，通过观察拟合的点进行判断，使其对表层 0.3 15
温度分布曲线既不能因多项式阶数取得过多产生 0.2
“过拟合”也不能取简单线性函数产生“欠拟合”。对 6
0.1 5 15
于深度 1000 m 以下温度可近似看成随深度线性变 7
0
化函数进行线性拟合。 4 5 6 7 8 9 10 11 12 13 14 15 16
CTD฾ባͯᎶ
10
图 3 拟合均方根误差
Fig. 3 The root mean square error of temperature
1
500 2
3 fitting
4
5 6
ງए/m 1000 7 8 从图 4 可以得到，在整个测区内盐度变化范围
9
10 都很小，因此在对盐度进行外推时，可以利用各深度
11 盐度均值作为外推的盐度数据 [2] 。最后采用式 (1)
12
1500 13
14 计算声速剖面。
15
16
17
10
2000
0 5 10 15 20 25 30
ພए/C
500 1
图 2 CTD 站位温度 2 3
4
Fig. 2 The temperature of CTD stations 5 6
ງए/m 1000 7
多项式拟合： 8 9 10
11
12
n−1
n
Y = a n X + a n−1 X + · · · + a 1 X + a 0 , (2) 1500 13
14
15
其中，n 为多项式的次数；Y 为拟合部分的实测声速 16
17
(单位：m/s)；X 为对应Y 的水深值(单位：m)。 2000 34.0 34.2 34.4 34.6 34.8 35.0 35.2 35.4 35.6 35.8 36.0
线性拟合： ᄢए/ā
p 1 × Z + p 2
T = 2 , (3) 图 4 CTD 站位盐度
Z + q 1 × Z + q 2
Fig. 4 The salinity of CTD stations
其中，T 为温度 (单位：C)，Z 为深度 (单位：m)，p 1 、
◦
p 2 、q1以及q 2 为参数。 1.2 BOA_Argo数据集
拟合均方根(Root mean square, RMS) 误差： 近几十年来，国际上出现了许多大范围、大规
v 模的海洋观测计划及系统，其中覆盖范围最广、规
u
1 ∑
u M [ ]
′
RMS = t T (Z i ) − T (Z i ) , (4) 模最大、数据最完善当属全球海洋实时观测网计划
M
i=1 (Argo) [9] 。这个项目由美国、英国、法国等国家的大
式 (4) 中，M 为深度点数，T (Z i ) 为 CTD 测量温度， 气和海洋科学家在 1998年提出，并迅速得到其他国
T ′ 为拟合温度。 家的积极响应。Argo 计划推出是为了实现快速测
(Z i )