Page 53 - 《应该声学》2022年第2期

第 41 卷 第 2 期 王磊磊等： 基于听觉谱特征的变压器绕组状态检测研究 221

0.10 0.09
0.08
0.10 0.08 0.10 0.07
ࣨϙ/mV 0.05 0.06 ࣨϙ/mV 0.05 0.06
0.05
0.04 0.04
0 0
0.5 0.5 0.03
0.4 0.02 0.4 0.02
0.3 0.3 0.01
20 20
0.2 15 0 0.2 15 0
0.1 10 ௑ᫎ/s 0.1 10
௑ᫎ/s
5 ྲढ़ᮠဋऀՂ 5 ྲढ़ᮠဋऀՂ
0 0
(a) 20%ᮕጋҧ (b) 60%ᮕጋҧ
0.08 0.10
0.10 0.07 0.10 0.08
ࣨϙ/mV 0.05 0.06 ࣨϙ/mV 0.05 0.06
0.05
0.04
0 0 0.04
0.5 0.03 0.5
0.4 0.02 0.4
0.3 0.3 0.02
20 0.01 20
0.2 15 0.2 15
0.1 10 0 ௑ᫎ/s 0.1 10 0
௑ᫎ/s
5 ྲढ़ᮠဋऀՂ 5 ྲढ़ᮠဋऀՂ
0 0
(c) 100%ᮕጋҧ (d) 140%ᮕጋҧ
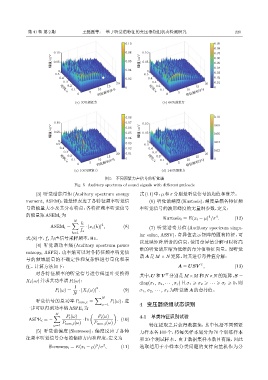
图 5 不同预紧力声信号的听觉谱
Fig. 5 Auditory spectrum of sound signals with different preloads
(3) 听觉谱能量矩 (Auditory spectrum energy 式(11)中，µ和σ 分别是听觉信号的均值和准差。
moment, ASEM)，能量矩表达了各特征频率听觉信 (6) 听觉谱峭度 (Kurtosis)，峭度是描各特征频
号的能量大小及其分布特点，各特征频率听觉信号 率听觉信号的波形峰度的无量纲参数，定义：
的能量矩ASEM i 为 4 4
Kurtosis i = E(x i − µ) /σ . (12)
N
∑ k
2
ASEM i = · |x i (k)| , (8) (7) 听觉谱奇异值 (Auditory spectrum singu-
f s
k=1 lar value, ASSV)，奇异值表示矩阵的固有特征，可
式(8)中，f s 为声信号采样频率，Hz。
以反映矩阵所含的信息，使用奇异值分解可以将高
(4) 听觉谱功率熵 (Auditory spectrum power
维的听觉谱压缩为低维的奇异值特征向量。设听觉
entropy, ASPE)，功率熵可以对各特征频率听觉信
谱A是M × N 矩阵，对其进行奇异值分解：
号的频域能量的不确定性和复杂性进行量化和表
T
征。计算方法如下： A = USV , (13)
对各特征频率的听觉信号进行傅里叶变换得 T
其中，U 和V 分别是M ×M 和N ×N 的矩阵，S =
X i (.ω)并求其功率谱P i (ω)：
diag(σ 1 , σ 2 , · · · , σ r ) 且 σ 1 > σ 2 > · · · > σ r > 0，则
1 2
P i (ω) = · |X i (ω)| . (9) σ 1 , σ 2 , · · · , σ r 为听觉谱A的奇异值。
N
∑ N
听觉信号的总功率 P sum,i = P i (ω)，进
ω=1 4 变压器绕组状态识别
一步可以得到功率熵ASPE i 为
N ( )
∑ P i (ω) P i (ω) 4.1 单类特征识别试验
ASPE i = − · ln . (10)
P sum,i (ω) P sum,i (ω)
ω=1 特征提取之后获得数据集，其中包括不同预紧
(5) 听觉谱偏度 (Skewness)，偏度反应了各特 力样本各 100 个，将每类样本划分为 70 个训练样本
征频率听觉信号分布的偏移方向和程度，定义为 和 30 个测试样本。由于数据集样本数目有限，因此
3
3
Skewness i = E(x i − µ) /σ , (11) 选取适用于小样本分类问题的支持向量机作为分