Page 39 - 《应用声学》2022年第4期

第 41 卷 第 4 期 钟华等： 激光超声的多模式合成孔径聚焦成像仿真分析 537

༏ԧ-ଊ฾ག(ੳଡ) 的幅值则无明显变化，与超声 B 扫结果相比实现了
√
x i
N 倍的信噪比提升，提高了缺陷图像的对比度和
横向分辨率。
使用单模式波进行 SAFT 时，会遇到因其他模
d i
式波干扰引起的伪像以及由激光超声方向性导致
的检测盲区等问题，为解决这些问题，本文提出了一
种基于激光超声的多模式 SAFT 方法，下面将介绍
多模组合方法以及模式选取的规则。
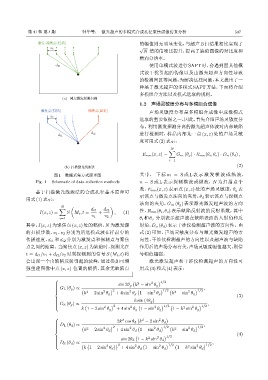
(a) Տག༏ԧଊ฾ੳଡ
1.2 声场灵敏度分布与多模组合成像
༏ԧག(ੳଡ) ଊ฾ག(ڍࠀ) 声场灵敏度分布是多模组合成像中成像模式
x i
选取的重要依据之一，因此，首先介绍声场灵敏度分
布。利用激发探测分离的激光超声体波对内部缺陷

d i 进行检测时，样品内部某一点 (x, z) 处的声场灵敏
d i
度可用式(2)表示：
N
∑
E mn (x, z) = G m (θ g ) · R mn (θ i , θ o ) · D n (θ d ) ,
i=1
(2)
(b) ੳଡ༏Аጳູข
图 1 数据采集方式原理图 其 中， 下 标 m = S 或 L 表 示 激 发 横 波 或 纵 波，
Fig. 1 Schematic of data collection methods n = S 或 L 表示探测横波或纵波，N 为扫描点个
数，E mn (x, z) 表示点 (x, z) 处的声场灵敏度，θ g 表
基于扫描激光线源法的合成孔径基本原理可
示该点与激发点法向的夹角，θ d 表示该点与探测点
用式(1)表示：
法向的夹角，G m (θ g ) 表示激光激发超声波的方向
N ( )
∑ d i1 d i2 性，R mn (θ i , θ o ) 表示缺陷反射波的反射系数，其中
I(x, z) = S M i , t = + , (1)
v 1 v 2
i=1 θ i 和 θ o 分别表示超声波在缺陷表面的入射角和反
其中，I(x, z) 为聚焦点 (x, z) 处的幅值，N 为激发源 射角，D n (θ d ) 表示干涉仪检测超声波的方向性。由
的扫描步数，v 1 、v 2 分别为所选模式波在样品中的 式 (2) 可知，声场灵敏度分布与激光激发超声的方
传播速度，d i1 和 d i2 分别为激发点和探测点与聚焦 向性、干涉仪检测超声的方向性以及超声波与缺陷
点之间的距离。当聚焦点(x, z)为缺陷时，探测光在 作用后的声场分布有关，声场灵敏度幅值越大，则信
t = d i1 /v 1 + d i2 /v 2 时刻探测到的信号 S (M i , t) 将 号幅值越强。
会出现一个由缺陷反射引起的波峰，通过叠加可增 激光激发超声和干涉仪检测超声的方向性可
强重建图像中点 (x, z) 位置的幅值，其余无缺陷点 用式(3)和式(4)表示：


( 2 2 ) 1/2

 sin 2θ g k − sin θ g

 G L (θ g ) ∝ ,
 ( ) 2 ( ) 1/2 ( ) 1/2
 2 2 2 2 2 2
k − 2 sin θ g + 4 sin θ g 1 − sin θ g k − sin θ g
(3)
 k sin (4θ g )


 G S (θ g ) ∝ ,
 ( ) 2 ( ) 1/2 ( ) 1/2
 2 2 2 2 2
k 1 − 2 sin θ g + 4 sin θ g 1 − sin θ g 1 − k sin θ g
 ( )
2 2 2
2k cos θ d k − 2 sin θ d


 D L (θ d ) ∝ ,
 ( ) 2 ( ) 1/2 ( ) 1/2
 2 2 2 2 2 2
 k − 2 sin θ d + 4 sin θ d 1 − sin θ d k − sin θ d
(4)
( ) 1/2
 2 2
 sin 2θ d 1 − k sin θ d


 D S (θ d ) ∝ ,
 ( ( 2 )) 2 2 ( 2 ) 1/2 ( 2 2 ) 1/2
k 1 − 2 sin θ d + 4 sin θ d 1 − sin θ d 1 − k sin θ d