Page 17 - 《应用声学》2022年第5期

第 41 卷 第 5 期 林基艳等： 周期性扇形孔结构对斜槽型纵扭复合模态超声振动系统性能的影响 693

由图 7 能够看出， 当特征频率为 12226 Hz、 从图 8 可以看出，基于周期性扇形孔和斜槽
18750 Hz 时，纵扭复合超声振动系统表现为以 结构的系统的旋转角度从 3.951 到 4.111 ，最大
◦
◦
纵振为主的振动型态；当特征频率为 7896.6 Hz、 旋转角度是没有扇形孔系统的 1.571 倍，平均旋
11336 Hz、17477 Hz 时，系统则表现为以扭振为主 转角度是没有扇形孔系统的 1.595 倍；扭转振幅从
的振动型态。与基于斜槽结构纵扭复合超声振动 0.0672 mm 到 0.0728 mm，其中，最大扭转振幅是
系统相同，也以二阶扭转模态为例，计算基于周期 无扇形结构的 1.580 倍，平均扭转振幅是无扇形结
7
2
性扇形孔和斜槽结构的系统与仅基于斜槽结构的 构的 1.598 倍；剪切应力从 0.435 × 10 N/m 变化
2
7
系统二者辐射面的扭转分量对比，结果如图 8 所示。 到3.16 × 10 N/m ，最大剪切应力是没有扇形孔系
统的 1.785 倍，平均剪切应力是没有扇形孔系统的
4.2
1.598倍，即引入扇形孔结构的系统的扭转分量得到
4.0
了有效的提升。另外，为了更加清晰地看到扇形孔
3.8
3.6 ۳̆பയፇ౞ᄊጇፒ 结构对系统性能的提升，图 9 给出了扇形片上的旋
஽ᣁᝈए/(O) 3.4 ۳̆ևరভ੡ॎߘ֗பയፇ౞ᄊጇፒ 转角度和剪切应力的曲线分布。
3.2
6.5
3.0
10.0
2.8 6.0 ஽ᣁᝈए
ҝѭऄҧ
2.6 5.5 8.0
2.4 5.0
0 5 10 15 20 25 30 6.0
ऻ᫂/mm ஽ᣁᝈए/(O) 4.5 ҝѭऄҧ/(10 7 NSm -2 )
(a) ஽ᣁᝈएࠫඋ 4.0 4.0
0.075 3.5
2.0
0.070 3.0
2.5 0
0.065 0 2 4 ᫂ए/mm 8 10 12
6
ੵᣁ૝ࣨ/mm 0.060 ۳̆பയፇ౞ᄊጇፒ 图 9 扇形片上的旋转角度和剪切应力
۳̆ևరভ੡ॎߘ֗பയፇ౞ᄊጇፒ
0.055
0.050 Fig. 9 Rotation angle and shear stress on the sector
0.045
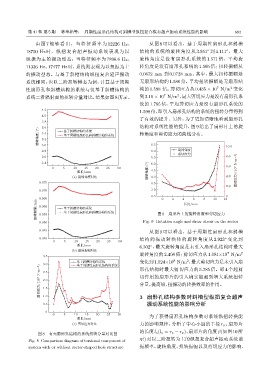
从图 9 可以看出，基于周期性扇形孔和斜槽
0.040 结构的振动转换体的旋转角度从 2.923 变化到
◦
0 5 10 15 20 25 30
ऻ᫂/mm
6.302 ，最大旋转角度是未引入扇形孔结构时最大
◦
(b) ੵᣁ૝ࣨࠫඋ
7
旋转角度的 2.408 倍；剪切应力从 1.081×10 N/m 2
3.5
8
2
۳̆பയፇ౞ᄊጇፒ 变化到1.024×10 N/m ，最大剪切应力是未引入扇
3.0
ҝѭऄҧ/(10 7 NSm -2 ) 2.5 切作用的扇形片的引入确实能起到增大系统扭转
۳̆ևరভ੡ॎߘፇ౞ᄊጇፒ
形孔结构时最大剪切应力的 5.785 倍。即 4 个起剪
2.0
分量，提高纵、扭振动的转换效率的作用。
1.5
1.0
振动系统性能的影响分析
0.5 3 扇形孔结构参数对斜槽型纵扭复合超声
0
0 5 10 15 20 25 30 为了获得扇形孔结构参数对系统纵扭转换能
ऻ᫂/mm
(c) ҝѭऄҧࠫඋ 力的影响规律，分析了中心小圆的半径 r x 、扇形片
的长度 l s (l s = r s − r x )、扇形片的角度 β(如图 10 所
图 8 有无扇形孔结构的系统扭转分量对比图
示) 对以二阶扭转为主的纵扭复合超声振动系统谐
Fig. 8 Comparison diagram of torsional component of
system with or without sector-shaped hole structure 振频率、旋转角度、扭转振幅以及剪切应力的影响，