Page 139 - 《应用声学》2022年第6期

第 41 卷 第 6 期 黄逸群等： 混凝土声发射信号源定位精度的细观模型计算分析 985

ܦԧ࠱͜ਖ٨4 ܦԧ࠱͜ਖ٨3 300
250

200

150
ܦԧ࠱ηՂູ
100

50

ܦԧ࠱͜ਖ٨1 ܦԧ࠱͜ਖ٨2 0 0 100 200 300
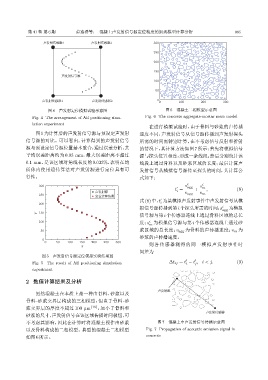
图 4 声发射定位模拟试验示意图 图 6 混凝土二相模型示意图
Fig. 4 The arrangement of AE positioning simu- Fig. 6 The concrete aggregate-mortar meso model
lation experiment
在进行模拟试验时，由于骨料与砂浆的声传播
图5 为计算后的声发射信号源与预设定声发射 速度不同，声发射信号从信号源传播到声发射探头
信号源的对比。可以看出，计算得到的声发射信号 所需的时间需特别计算，在不考虑信号反射和折射
源与预设定信号源位置基本重合，通过误差分析，其 的情况下，其计算方法如图 7 所示：首先将模拟信号
平均误差距离约为 0.03 mm，最大误差距离不超过 源与探头位置相连，形成一条线段；然后分别统计该
0.1 mm，是该区域对角线长度的 0.033%，表明在均 线段上通过骨料以及砂浆区域的长度；最后计算声
质体内使用遗传算法对声发射源进行定位具有可 发射信号从模拟信号源传至探头的时间，其计算公
行性。 式如下：

300 s i agg s i m
t = + , (8)
′
ܦԧ࠱ູ i v agg
250 ࠀͯᝠካፇ౧ v m
式(8)中，t 为某模拟声发射事件中声发射信号从模
′
200 i
拟信号源传播到第i个探头所需的时间；s i agg 为模拟
Y 150
信号源与第 i 个传感器连线上通过骨料区域的总长
度；s 为模拟信号源与第 i 个传感器连线上通过砂
100 i
m
浆区域的总长度；v agg 为骨料的声传播速度；v m 为
50
砂浆的声传播速度。
0
0 50 100 150 200 250 300 则各传感器测得的同一模拟声发射事件时
X
间差为
图 5 声发射信号源定位模拟实验结果图
′
′
Fig. 5 The result of AE positioning simulation ∆t ij = t − t , i < j. (9)
j
i
experiment
2 数值计算结果及分析
ܦԧ࠱ູ
虽然混凝土在本质上是一种由骨料、砂浆以及
骨料 -砂浆交界层构成的三相模型，但由于骨料 -砂
浆交界层的厚度不超过 100 µm [15] ，远小于骨料和
ܦԧ࠱͜ਖ٨
砂浆的尺寸，声发射信号在该区域传播时间极短，可
不考虑其影响，因此在计算时将混凝土视作由砂浆 图 7 混凝土中声发射信号传播示意图
以及骨料构成的二相模型。典型的混凝土二相模型 Fig. 7 Propagation of acoustic emission signal in
如图6所示。 concrete