Page 43 - 《应用声学》2022年第6期

第 41 卷 第 6 期 宋晓等： 机体表面湍流边界层噪声特性及预测方法研究 889

200 ∼ 2000 Hz，主要在于 Robertson 模型所计算的
频谱弯曲程度低于试验结果，表明参数 A 的默认取
5 dB 值偏小。
Ҫဋ៨/dB

A/⊲֒ B/֒ C/⊲
A/⊲֒ B/֒ C/⊲
↼Robertsonവی↽ 5 dB
Ҫဋ៨/dB
A/֒ B/֒ C/⊲
20 200 2000
ࢺц2តᰎϙ
ᮠဋ/Hz
Robertsonവی
(a) Ԡ஝Aԫӑ Cockburn & Robertsonവی
20 200 2000
ᮠဋ/Hz
5 dB (a) 2Ղ฾ག
Ҫဋ៨/dB

A/⊲֒ B/֒ C/⊲
A/⊲֒ B/֒ C/⊲ 5 dB
Ҫဋ៨/dB
↼Robertsonവی↽
A/⊲֒ B/֒ C/⊲
20 200 2000 ࢺц2តᰎϙ
ᮠဋ/Hz Robertsonവی
(b) Ԡ஝Bԫӑ Cockburn & Robertsonവی
20 200 2000
ᮠဋ/Hz
(b) 8Ղ฾ག
Ҫဋ៨/dB 5 dB 图 10 工况 2 下试验值和预测值对比

A/⊲֒ B/֒ C/⊲ Fig. 10 Comparison of test value and predictive
↼Cockburn & Robertsonവی↽
value at Condition 2
A/⊲֒ B/֒ C/⊲
↼Robertsonവی↽
A/⊲֒ B/֒ C/ 为了优化 Robertson 模型中的参数，保持参数
C = 0.6366 不变，通过最小二乘法得到新的参数 A
20 200 2000
ᮠဋ/Hz 值、B 值，见表3、表4。可以看出，基于试验数据拟合
(c) Ԡ஝Cԫӑ
的 A 值、B 值和 Robertson 模型中的默认值有一定
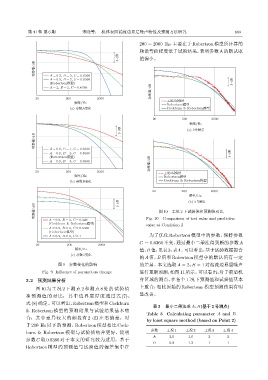
图 9 参数变化的影响 的差异。本文选取A = 2、B = 1 对湍流边界层噪声
Fig. 9 Influence of parameters change 进行重新预测，如图11所示。可以看出，对于前后机
3.2 预测结果分析 身区域的测点，在各个工况下预测值和试验值基本
图 10 为工况 2 下测点 2 和测点 8 处的试验值 上重合，相比原始的 Robertson 模型预测结果有明
和预测值的对比， 其中边界层厚度通过式 (7)、 显改善。
式 (8)确定。可以看出，Robertson模型和Cockburn
表 3 最小二乘法求 A、B(基于 2 号测点)
& Robertson 模型的预测结果与试验结果基本吻
Table 3 Calculating parameter A and B
合，其中差异较大的频段有 2 dB 左右偏差。对
by least square method (based on Point 2)
于 200 Hz 以下的预测，Robertson 模型相比 Cock-
参数 工况 1 工况 2 工况 3 工况 4
burn & Robertson 模型与试验值吻合更好，说明
A 2.6 1.6 2 2
参数 C 取 0.6366 对于本文的研究较为适用。基于
B 0.8 1.3 1 1
Robertson 模型的预测值与试验值的偏差集中在