Page 42 - 《应用声学》2022年第6期

888 2022 年 11 月

′2
p = 0.006q ∞ , (3)
1 + 0.14Ma 2
5 dB ω 0 = 0.5 U ∞ , (4)
Ҫဋ៨/dB 其中，Ma为来流马赫数，U ∞ 为来流速度，δ 为边界
δ
∗
∗
5Ղ฾ག 层位移厚度，q ∞ 为来流动压。
6Ղ฾ག Cockburn & Robertson对Robertson模型的特
7Ղ฾ག
征频率进行了改写，发展的Cockburn & Robertson
20 200 2000 模型表达式如下 [4] ：
ᮠဋ/Hz
p ′2
ϕ(f) = ) , (5)
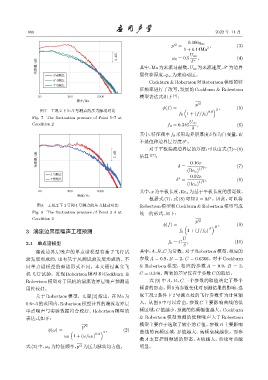
图 7 工况 2 下 5∼7 号测点的压力脉动对比 ( 0.9 2
f 0 1 + (f/f 0 )
Fig. 7 The fluctuation pressure of Point 5–7 at
Condition 2 f 0 = 0.346 U ∞ , (6)
δ
其中，特征频率f 0 采用边界层厚度δ 作为自变量，而
不是位移边界层厚度δ 。
∗
对于平板湍流边界层的厚度，可以由式(7)∼(8)
Ҫဋ៨/dB 5 dB 估算 [17] ： 0.16x

δ =
(Re x ) 1/7 , (7)
3Ղ฾ག 0.02x
∗
4Ղ฾ག δ = , (8)
(Re x ) 1/7
20 200 2000 其中，x为平板长度，Re x 为基于平板长度的雷诺数。
ᮠဋ/Hz
根据式 (7)、式 (8) 可知 δ = 8δ 。因此，可以将
∗
图 8 工况 2 下 3 号和 4 号测点的压力脉动对比 Robertson模型和Cockburn & Robertson模型写成
Fig. 8 The fluctuation pressure of Point 3–4 at 统一的形式，如下：
Condition 2 ′2
p
ϕ(f) = ) , (9)
( B
A
3 湍流边界层噪声工程预测 f 0 1 + (f/f 0 )
U
3.1 单点谱模型 f 0 = C δ , (10)
湍流边界层噪声的单点谱模型有基于飞行试 其中，A、B、C 为常数。对于Robertson模型，相应的
验发展形成的，也有基于风洞试验发展形成的。不 参数 A = 0.9，B = 2，C = 0.6366。对于 Cockburn
同单点谱模型的频谱形式不同。本文通过真实飞 & Robertson 模型，相应的参数 A = 0.9，B = 2，
机飞行试验，发现 Robertson 模型和 Cockburn & C = 0.346。两者的差异仅在于参数C 的取值。
Robertson 模型对于民机的湍流边界层噪声预测适 式 (9) 中 A、B、C 三个参数的取值决定了整个
用性较好。 频谱的形态。图9为参数变化对预测结果的影响，选
关于 Robertson 模型，文献 [2] 指出，在 Ma 为 取工况 2 条件下 2 号测点处的飞行参数作为计算输
0.6∼3 的范围内，Robertson模型计算的湍流边界层 入。从图 9 中可以看出，参数 C 主要影响曲线的低
单点噪声与实验数据符合较好。Robertson 模型的 频区域，C 值越小，预测的低频幅值越大。Cockburn

表达式如下： & Robertson 模型预测的低频噪声大于 Robertson
模型主要在于选取了较小的C 值。参数B 主要影响
p ′2
ϕ(ω) = ( ) , (2) 曲线的高频区域，B 值越大，高频衰减越快。而参
2
0.9
ω 0 1 + (ω/ω 0 )
数 A 主要控制频谱的形态，A 值越大，曲线弯曲越
式(2)中，ω 0 为特征频率，p 为压力脉动均方值， 明显。
′2