Page 100 - 《应用声学》2023年第2期

288 2023 年 3 月

10 10 网络拓扑结构如图 10所示，其中隐含层神经元个数
N m 与输入 N i 、输出 N O 神经元之间的数量关系 [18]
፬ՌកѬ 6 6 为N m = 2N i + N O ，因此隐含层神经元个数为9。
8
8

4 4
0.1 0.2 0.3 0.4 0.1 0.2 0.3 0.4
ܦᑟ/Pa 2 ܦᑟ/Pa 2 ܦᑟ
100~200 Hz
(a) 100~200 Hz (b) 200~500 Hz
10 10 200~500 Hz ˟᜺
កѬ
500~2000 Hz ᣥѣࡏ
፬ՌកѬ 100~2000 Hz
ᇸፃЋ
8
8
6
6
ᣥКࡏ
ᇸፃЋ
4 4
0 0.1 0.2 0.3 0.2 0.4 0.6 0.8
ᬥեࡏ
ܦᑟ/Pa 2 ܦᑟ/Pa 2 ᇸፃЋ
(c) 500~2000 Hz (d) 100~2000 Hz
图 10 主客观映射神经网络拓扑结构
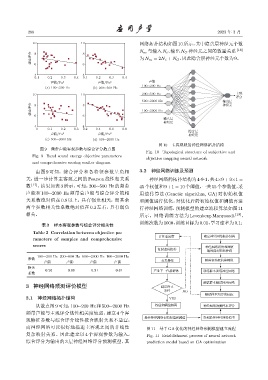
图 9 频带声能客观参数与综合评分散点图
Fig. 10 Topological structure of subjective and
Fig. 9 Band sound energy objective parameters
objective mapping neural network
and comprehensive scoring scatter diagram
由图 9 可知，综合评分和各特征参数呈负相 3.2 神经网络训练及预测
关，进一步计算主客观之间的 Pearson 线性相关系 神经网络的拓扑结构为4-9-1，共4×9 + 9×1 =
数 [17] ，结果如表 3 所示，可知：200∼500 Hz 的频带 45个权值和9+1 = 10个阈值，一共55个参数值，采
声能和 100∼2000 Hz 频带总声能与综合评分的相 用遗传算法 (Genetic algorithm, GA) 对初始权值
关系数绝对值在 0.8 以上，具有强负相关，而其余 和阈值进行优化，对优化后的初始权值和阈值再进
两个参数相关性系数绝对值在 0.3 左右，具有弱负 行神经网络训练，预测模型的建立流程算法如图 11
相关。 所示。网络训练方法为 Levenberg-Marquardt [18] ，
训练次数为1000，训练目标为0.01，学习速率为0.1；
表 3 样本客观参数与综合评分相关性
Table 3 Correlation between objective pa-
ᝠካᤠऄए ᆸࠀᇸፃᎪፏ઩੨ፇ౞
rameters of samples and comprehensive
scores ᇸፃᎪፏిϙ֗᫠ϙ
ܭ҄᥌͜୲ͻ ᎄᆊ४҂ѺݽመᏆ
100∼200 Hz 200∼500 Hz 500∼2000 Hz 100∼2000 Hz
参数 ̔Ԣ୲ͻ ᝍᆊѺݽిϙ֗᫠ϙ
声能 声能 声能 声能
相关
−0.26 −0.86 −0.31 −0.81 ̗ၷʾʷ̽ழᏆʹ ᝫጷನవᝫጷᇸፃᎪፏ
系数
฾តನవ฾តᇸፃᎪፏ
3 神经网络预测评价模型 ໘ᡜጼൣ
౎͈ NO
฾តನవکவϙ.4&
3.1 神经网络拓扑结构 YES
从散点图 9 可知：100∼200 Hz 和 500∼2000 Hz ిϙ֗᫠ϙᝍᆊ ᇸፃᎪፏᮕ฾ನవកѬ
频带声能与主观评分线性相关度较弱，建立 4 个客
తΈᇸፃᎪፏѺݽిϙ֗᫠ϙ ४҂తጼᇸፃᎪፏവی
观特征参数与综合评分线性拟合映射关系不适宜，
而神经网络可以很好地描述主客观之间的非线性 图 11 基于 GA 优化的神经网络预测模型建立流程
复杂映射关系。因此建立以 4 个客观参数为输入， Fig. 11 Establishment process of neural network
综合评分为输出的 3 层神经网络评分预测模型，其 prediction model based on GA optimization