Page 209 - 《应用声学》2023年第3期

第 42 卷 第 3 期 靳伯骜等： 地表振动传感器质量对水平耦合谐频的影响 647

仿真。仿真模型与坐标系(x, y, z)如图2所示。仿真 图 2 中，弹簧与质量块的形状均为边长为 1 cm
中土壤的半径为 14 cm，外部被完美匹配层包裹，以 的立方体。依据表 1 的参数，激振器质量块的质量
4
此模拟外场实验场景。地表水平振源由一个铝杆和 为 57.6 g，弹簧的劲度系数为 1.35 × 10 N·m −1 ，传
动圈式电磁激振器构成，其中电磁激振器由质量块 感器质量记为 m。仿真中，水平振源、土壤以及传感
与弹簧表示，电磁激振器质量块的振动位移以 u s 表 器耦合工装构成了一个线性系统，简谐外力作为输
示，电磁力 F 施加于激振器质量块上，方向平行于 y 入量施加于振源质量块上。这一线性系统可分为杆
轴。传感器与铝质工装位于 x 轴上，与原点 O 的距 状水平振源与信号采集系统两部分。其中，归一化
离为5 cm，工装的埋地深度为 4 cm。传感器的本地 位移u a /u s 能够反映该系统的频率响应特性。
位移以 u a 表示。模型中的材料参数如表 1 所示，其 为了研究 m 对信号采集的影响，对比了频域仿
中土壤的参数来自文献[10]。 真中 m 取不同值的情况下，u a /u s 的幅值与相位随

表 1 模型参数 频率的变化关系，绘制于图 3。当 m = 0 g 时，只有
Table 1 The parameters of model 传感器工装固定于地表，其尺寸小于波长且密度与
土壤接近，这使得信号采集系统对 u a 的影响很小，
材料 密度/(kg·m −3 ) 杨氏模量/GPa 泊松比
u a 与该点处土壤的水平振动位移一致。在图 3(a)
铝 2.7 × 10 3 69.0 0.33
中，m = 0 g 所对应的曲线在 700 Hz 附近出现了共
土壤 2.0 × 10 3 5.33 × 10 −2 0.332
弹簧 1.3 1.35 × 10 −3 0.01 振峰，而图 3(b)中，m = 0 g所对应的曲线在该频率
激振器质量块 5.76 × 10 4 7.0 × 10 4 0.01 出现了相位的跃变，这表明仿真中振源在700 Hz 附
传感器质量块 7.0 × 10 4 0.01 近发生共振。

༏૝٨
u s ژܢ ߹ᎿӜᦡࡏ
᠏᧚ڱ
F a u a ͜ਖ٨
᠏᧚ڱ
ुዔ 7 cm
ᨸీ
O ᨸ҄ࢺᜉ
O

12 cm
z z
y x
O 1 cm O
y
ࠫሦ᣸ႍ
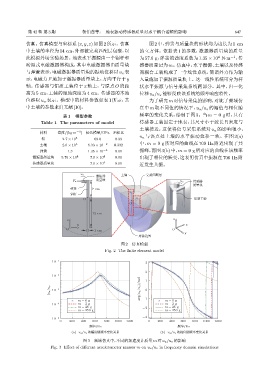
图 2 仿真模型
Fig. 2 The finite element model

10 -1
3
2
10 -2 1

|u a /u s | 10 -3 arg(u a /u s )/rad 0

m=0 g -1 m=0 g
10 -4 m=2 g m=2 g
m=25 g -2 m=25 g
m=250 g m=250 g
-3
10 -5
0 200 400 600 800 1000 1200 0 200 400 600 800 1000 1200
ᮠဋ/Hz ᮠဋ/Hz
(a) u a /u s ᄊࣨएᬤᮠဋԫӑТጇ (b) u a /u s ᄊᄱͯᬤᮠဋԫӑТጇ
图 3 频域仿真中，不同的加速度计质量 m 对 u a/u s 的影响
Fig. 3 Effect of different accelerometer masses m on u a/u s in frequency domain simulations