Page 97 - 《应用声学》2023年第4期

第 42 卷 第 4 期 孙志峰等： 随钻声波测井四极子发射换能器的设计 759

称分布。换能器两端的径向位移值与中部的径向位 所示。从图中对比可以看出，在频率为 7.5 kHz 以
移值反向，即换能器两端向里收缩时，换能器中部向 下金属基片结构换能器的发射电压响应远大于现
外扩张；换能器中心部位切向位移值为零，且向两端 用的随钻四极子发射换能器。金属基片结构换能
逐渐递增，两端端点处切向位移值最大；换能器任意 器在频率为 5.0 kHz 处对应的最大发射电压响应为
点的轴向位移值接近于零。从图 4(b) 可以看出，金 139.9 dB，对应该换能器在流体中的一阶弯曲振动，
属基片结构换能器的径向位移值、切向位移值、轴 由于流体负载作用的影响，该谐振频率低于换能器
向位移值也沿换能器中心点呈对称分布。换能器中 在空气中的弯曲振动谐振频率，表明金属基片结构
心部位径向位移值最大，且向两端逐渐递减，两端端 换能器的弯曲振动模式在声场的激发效率方面能
点处径向位移值趋近于零；换能器中心部位切向位 更好满足随钻四极子模式测量需求。
移值为零，且向两端逐渐递增，但两端端点处切向
150
位移值也很小；换能器任意点的轴向位移值接近于
140
零。这进一步表明金属基片结构的换能器弯曲振动 130
模式在位移值大小及声场分布上都能满足随钻四 120
TVR/dB 100
极子模式测量的需求。 110
3 90 ௄᧛࡛۳ྟ
80
2 ద᧛࡛۳ྟ
70
1
60
A/(10 -6 mm) -1 1 2 3 4 ᮠဋ/kHz 7 8 9 10
0
50
6
5
-2
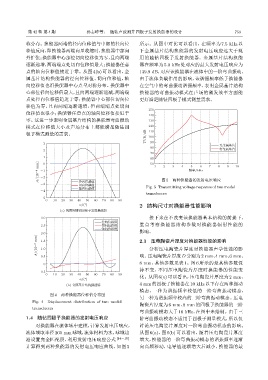
-3 य़Քͯረϙ 图 5 两种换能器的发射电压响应
ѭՔͯረϙ
ᣉՔͯረϙ Fig. 5 Transmitting voltage response of two model
-4
transducers
-5
0 10 20 30 40 50 60 70 80 90
α/(°) 2 结构尺寸对换能器性能影响
(a) ဘၹᄊᬤᨛپౝߕԧ࠱૱ᑟ٨
3.0 接下来在不改变该换能器基本结构的前提下，
य़Քͯረϙ
2.5 ѭՔͯረϙ 重点考察换能器结构参数对换能器辐射性能的
ᣉՔͯረϙ
2.0 影响。
A/(10 -5 mm) 1.5 2.1 分析压电陶瓷片厚度对换能器声学性能的影
压电陶瓷片厚度对换能器性能的影响
1.0

0.5 响。压电陶瓷片厚度D 分别为2 mm、4 mm、6 mm、
8 mm，其他参数见表 1。图 6 所示的是其他参数保
0
持不变，不同压电陶瓷片厚度时换能器的性能变
-0.5
0 10 20 30 40 50 60 70 80 90 化。从图 6(a) 可以看出，压电陶瓷片厚度为 2 mm、
α/(°)
(b) ᧛࡛۳ྟፇ౞૱ᑟ٨ 4 mm的四极子换能器在10 kHz以下存在两种振动
模态，一种为谐振频率较低的一阶弯曲振动模态，
图 4 两种换能器位移值分布图
另一种为谐振频率较高的三阶弯曲振动模态。压电
Fig. 4 Displacement distribution of two model
陶瓷片厚度为6 mm、8 mm 的四极子换能器的三阶
transducers
弯曲振动模态大于 10 kHz，在图中未绘制。由于三
1.4 随钻四极子换能器的发射电压响应 阶弯曲振动模态不适用于四极子测量模式，所以仅

对换能器在流体域中建模，计算发射电压响应， 讨论压电陶瓷片厚度对一阶弯曲振动模态的影响。
流体域取半径200 mm球域，流体材料为水，球域边 从图 6(a)、图 6(b) 可以看出，随着压电陶瓷片厚度
沿设置完全匹配层，利用发射电压响应公式 [14−15] 增大，换能器的一阶弯曲振动模态的谐振频率逐渐
计算得到两种换能器的发射电压响应曲线，如图 5 向高频移动，电导值逐渐增大后减小，换能器的最