Page 75 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 张邦： 超声阵列方法在层状结构损伤检测中的应用 967

式 (2) 中，|AB|、|AC| 分别为 AB 两点和 AC 两点间 到达时间时，先对成像区域进行网格划分(如图6 所
距离，φ为AB、AC 之间的夹角。 示)，用网格点代表成像点，对每一个回波记录，利
用无砟轨道现场实测的速度值，可以精确地计算成
O
像点到激发和接收点的传播最短时间 t S 、t G ，带入
TFM成像公式(1)即可得到成像点幅值。

A B
ϕ D 3 层间损伤定量分析

超声波在层状混凝土结构中传播，经过层间界
C
面时，层间接触状态的差异会导致超声波在结构面
图 7 由 A、B 两点时间插值求 C 点时间的几何关系 反射能量不同，当出现离缝、脱空时，反射能量会显
Fig. 7 The geometric relation of time at C is ob-
著增强。使用 TFM 可对层状无砟轨道混凝土结构
tained by interpolation of time at two points A, B
进行准确成像，但是对混凝土层间状态的评价只能
LTI方法通过网格剖分的方法计算超声波在结 根据反射面成像的能量幅值定性分析。本文基于超
构物内部传播时间，同样适用于任意已知复杂结 声波反射波信号和直达波信号进行能量特征分析，
构。图8 为利用射线追踪方法模拟得到的超声波在 计算界面密实度指标。
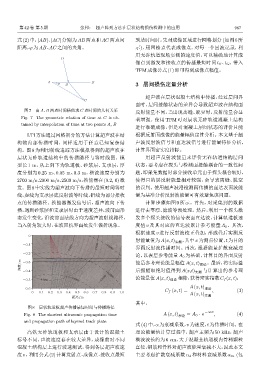
层状无砟轨道结构中的传播路径与等时线图。模 用超声反射波能量来评价无砟轨道结构层间
型长 1 m，从上到下为轨道板、砂浆层、支承层，厚 状态，要考虑在探头与检测面接触耦合的一致性问
度分别为 0.25 m、0.05 m、0.3 m，横波速度分别为 题，即采集数据时部分接收单元由于探头耦合较好，
2700 m/s、2000 m/s、2500 m/s，换能器在(0.2, 0)激 使得目的层反射能量相对较强，会导致离缝、脱空
发。图8 中实线为超声波向下传播的最短时间等时 的误判。使用超声波沿检测面传播的直达表面波能
线，虚线为支承层底反射波等时线，折线为部分接收 量为基准分析反射波能量可有效避免该问题。
点的传播路径。换能器激发信号后，超声波向下传 计算步骤如图 9 所示。首先，对采集到的数据
播，遇到砂浆层和支承层时由于速度差异，波前面形 进行去零漂、滤波等预处理。然后，利用一个探头激
态发生变化，沿波前面法线方向为超声波射线路径， 发多个探头接收的信号表面直达波，计算轨道板速
当入射角较大时，在波阻抗界面处发生偏折现象。 度值 v 及其对应的直达波累计参考能量 A 0 。其次，
根据速度 v 进行反射波校正叠加，形成叠后实测反
0
射能量值为A(x, t) 实测 ，其中x为测点位置，t 为目的
-0.1
0.0001 0.0002 0.0005 界面反射波传播时间。再次，根据能量扩散衰减理
-0.2
论，以表层参考能量 A 0 为基础，计算目的界面反射
␡ᓖ/m -0.3 能量参考理论能量幅值 A(x, t) 理论 。最后，将实际叠
与计算出的参考理
后振幅取绝对值得到 A(x,t)
-0.4
实测
0.0003 0.0004 论能量值A(x, t) 相除，获得密实指数C f (x, t)：
-0.5 0.0002 0.0003 理论
A (x, t)
-0.6 理论 (3)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 C f (x, t) = ,
A (x, t)
ᡰሏ/m 实测
其中，
图 8 层状轨道板超声传播最短时间与传播路径
Fig. 8 The shortest ultrasonic propagation time A (x, t) 理论 = A 0 · e −αvt , (4)
and propagation path of layered track plate
式(4) 中，α 为衰减系数，v 为速度，t为传播时间。在
高铁无砟轨道板和支承层由于设计的混凝土 理论能量值计算过程中，超声主频为 50 kHz，超声
标号不同，声波速度存在较大差异，成像前对不同 横波波长约为 6 cm，大于混凝土轨道板内骨料颗粒
混凝土结构层上进行波速测试，得到各层超声波速 直径，钢筋和骨料对超声波能量衰减不大，因此本文
度v。利用公式(2)计算发射点-成像点-接收点最短 主要考虑扩散衰减系数 α d 和材料衰减系数 α m (包