Page 74 - 《应用声学）》2023年第5期

966 2023 年 9 月

为接收阵元编号 (i < j 6 N)。按此方式每个探头
发射时，其右边所有探头接收信号，最终得到半矩阵 ௑ᫎ/ms
数据，如图4(b)所示。
完成一次采集共可以得到66道数据，实现该线
性阵列的半矩阵数据采集，如图 5所示，图中超声直 R i↼t i↽
达波和反射波明显，蓝线为前两个探头激发时的表
S G
面直达波，红线为层状介质界面反射波信号。
ᡰሏ/m
T S
T g

M

(a) ᡔܦ᫼ѵӧᅾ᫼஝૶᧔ᬷᇨਓ
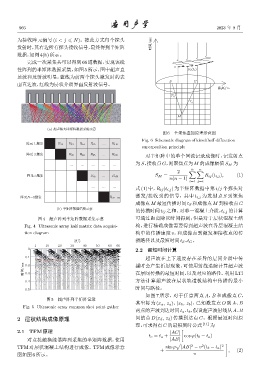
图 6 全聚焦叠加原理示意图
Fig. 6 Schematic diagram of kirschhoff diffraction
᫼Ћ  ༏ԧ R  R  R  R  ⊲⊲⊲ R N
superposition principle
᫼Ћ  ༏ԧ ⊲⊲⊲
对半矩阵中的单个回波记录成像时，记发射点
R 
R N
R 
R 
为S，接收点G，则聚焦点为M 的成像幅值S M 为
⊲⊲⊲ ⊲⊲⊲ ⊲⊲⊲ ⊲⊲⊲ ⊲⊲⊲
n n
2 ∑ ∑
᫼Ћ i ༏ԧ R i ⊲⊲⊲ R iN S M = R ij (t i,j ), (1)
n(n − 1)
i=1 j=i
⊲⊲⊲ ⊲⊲⊲ ⊲⊲⊲
式 (1) 中，R ij (t i,j ) 为半矩阵数据中第 i/j 个探头对
᫼ЋN֓༏ԧ R N֓N 激发/接收到的信号，其中 t i,j 为发射点 S 到聚焦
成像点M 最短传播时间t S 和成像点M 到接收点G
(b) ӧᅾ᫼஝૶ፇ౞ᇨਓ
的传播时间t G 之和。对单一混凝土介质，t i,j 的计算
图 4 超声阵列半矩阵数据采集示意 可通过距离除以时间得到；但是对于层状混凝土结
Fig. 4 Ultrasonic array half matrix data acquisi- 构，进行精确成像需要得到超声波在各层混凝土结
tion diagram 构中的传播速度 v，和成像点到激发和接收点的传
᥋Ղ 播路径以及最短时间t S 、t G 。
1 10 20 30 40 50 60 66
0 2.2 最短时间计算

0.1 超声波在上下速度存在差异的层间介质中传
௑ᫎ/ms 0.2 播时会产生折射现象，可使用射线追踪计算超声波

在层间传播的最短时间，以及对应的路径。利用LTI
0.3
0.4 方法计算超声波在层状轨道板结构中传播的最小
时间与路径。
0.5
如图 7 所示，对于任意两点 A、B 和成像点 C，
图 5 超声阵列半矩阵记录
其坐标为 (x a , z a )、(x b , z b )，已知激发点 O 到 A、B
Fig. 5 Ultrasonic array common shot point gather
两点的声波到达时间t a 、t b ，假设超声波射线从A、B
2 层状结构成像原理 间的点 D(x d , z d ) 传播到达点 C。根据最短时间原
理，可求得点C 的最短到时公式 [11] 为
2.1 TFM原理 |AC| [
t c = t a + cos φ(t b − t a )
对点接触换能器阵列采集的半矩阵数据，使用 |AB|
√ ]
2
2
TFM 对层状混凝土结构进行成像。TFM 成像示意 sin φ |AB| − v (t b − t a ) 2
+ , (2)
图如图6所示。 v