Page 33 - 201806

第 37 卷 第 6 期 周文佳等： 级联积分梳状滤波器在超声检测系统中的应用 863

与滑动平均滤波器的传递函数完全相同。同时可 N × 13.46 dB，随之带来的负面影响是通带内衰减
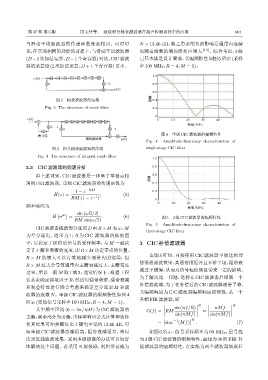
见，在实现相同的功能的前提下，与滑动平均滤波器 也随着级数的增加而相应增大 [10] 。综合考虑，3 级
(D −1次加法运算、D −1个寄存器)对比，CIC滤波 已基本满足设计要求，其幅频特性如图5 所示(采样
器的运算量(2次加法运算、D + 1个寄存器)更少。 率100 MHz，R = 4，M = 1)。

1.0
x↼k↽
 ֓ 0.8
y↼k↽
0.6
图 2 梳状滤波器的结构 ૝ࣨ 0.4
Fig. 2 The structure of comb filter 0.2

0
x↼k↽ 0 10 20 30 40
ᮠဋ/MHz
b/
 ֓
图 4 单级 CIC 滤波器的幅频特性
ሥѬ٨
೛࿄໚ฉ٨ y↼k↽
Fig. 4 Amplitude-frequency characteristics of
图 3 积分梳状滤波器的结构 single-stage CIC filter
Fig. 3 The structure of integral comb filter
1.0
2.3 CIC滤波器的频谱分析 0.8
由上述可知，CIC 滤波器是一种基于零极点相 0.6
消的FIR滤波器。单级CIC滤波器的传递函数为 ૝ࣨ 0.4
1 − z −RM 0.2
H(z) = , (5)
RM (1 − z −1 ) 0
0 10 20 30 40
频率响应为 ᮠဋ/MHz
( ) sin (ωR/2)
H e jω = . (6) 图 5 3 级 CIC 滤波器的幅频特性
RM sin(ω/2)
Fig. 5 Amplitude-frequency characteristics of
CIC滤波器梳状部分延迟D 由R × M 表示：M
three-stage CIC filter
为差分延迟，通常为 1；R 为 CIC 滤波器的插值因
子，它决定了插值后信号的采样频率，与 M 一起决 3 CIC补偿滤波器
定了主瓣和旁瓣的宽度，即R×M 决定零点的位置。
由图 5 可知，直接使用 CIC 滤波器不能达到理
R × M 的增大可以有效地减少通带内的混叠，但
想低通滤波效果，其通带很短并且不够平坦，阻带衰
R × M 过大会导致通带内主瓣衰减过大、主瓣宽度
减过于缓慢，从而对信号幅值恢复带来一定的影响。
过窄，所以一般 M 取 1 或 2；通常情况下，根据工程
为了解决这一问题，选择在 CIC 滤波器后级联一个
要求来确定抽取因子R，然后对通带带宽、通带衰减
补偿滤波器，为了使补偿后的CIC滤波器通带平整，
和混叠特性进行综合考虑来确定差分延迟 M 和滤
其幅频响应为 CIC 滤波器幅频响应的倒数，是一个
波器的级数 N。单级 CIC 滤波器的幅频特性如图 4
升幅FIR滤波器，即
所示(原始信号采样率100 MHz，R = 4，M = 1)。

N N
其中频率区间 (0 ∼ 2π/RM) 为 CIC 滤波器的 G(f) = RM sin(πf/R) ≈ πMf

sin(πMf) sin(πMf)
主瓣，剩余部分为旁瓣，由频率响应公式计算和软件
−1 N

仿真结果可知旁瓣仅比主瓣电平低约 13.46 dB，可 = sinc (Mf) . (7)
知单级 CIC 滤波器旁瓣很高，阻带衰减很差，难以 如图 6 所示，信号采样频率为 50 MHz，星号线
达到低通滤波效果。采用多级级联的办法可以较好 为3级CIC滤波器的幅频特性，虚线为30阶FIR 补
地解决这个问题。若采用 N 级级联，则阻带衰减为 偿滤波器的幅频特性，点实线为两个滤波器级联后