Page 118 - 应用声学2019年第2期

264 2019 年 3 月

D
d

ܦູ᭧ ੳଡ᭧ ᫼ѵ᭧

图 1 随机传声器阵列阵元分布图 图 2 仿真示意图
Fig. 1 Random microphone position map Fig. 2 Schematic diagram of simulation

源所在平面、扫描面、阵列面，其中，声源面到扫描 增强趋势，但聚焦程度仍然低。
面 距离为d，声源面到阵列面距离为D = 1 m不变。 图 3(b)、图 3(d)、图 3(f) 为基于 Group Lasso 的
距离 d 是由于声源位置测量不准确导致的误差，在 MUSIC 算法优化结果，从这三幅图中可以看出，优
实际应用中，可能由于环境原因无法准确获取真实 化后的MUSIC算法声源定位效果受频率影响极小。
的距离D。 Group Lasso MUSIC 算法经过对声源点稀疏筛选，
聚焦性能较MUSIC算法有极大提高。
2.2 仿真分析
在单声源仿真基础上，将声源增加为双声源验
2.2.1 仿真1 证算法对多声源声场环境适应性及稳定性。图4(a)、

设置声源为点声源，位于原点位置，信噪比为 图 4(c)、图 4(e) 分别为双声源 MUSIC 算法 200 Hz、
5 dB，声源面到扫描面距离 d = 0，声源面到阵列面 600 Hz、1000 Hz的计算结果，相较于单声源，双声源
距离 D = 1 m，分析在中低频声源情况下，Group MUSIC算法结果分辨率要差。经Group Lasso算法
Lasso MUSIC 算法的优化效果。单声源优化结果 优化后，如图4(b)、图4(d)、图4(f)，对于200 Hz仿真
如图 3 所示，图3(a)、图 3(c)、图 3(e)分别为 200 Hz、 结果，稀疏程度并没有其他两者高，但主瓣宽度明显
600 Hz、1000 Hz 时 MUSIC 算法计算结果，从这三 下降，分辨率显著提高。600 Hz 与 1000 Hz 优化效
幅图中可看出，随着声源频率提高，声源位置的分辨 果较好，分辨率提升明显，本文算法对中低频多声源
程度逐渐提高，声源主瓣宽度逐渐缩小，聚焦性能呈 环境有较好的适应性，效果稳定。

0.5 1.00 0.5 1.0 0.5
0.8
0.8
0.95
0 0 0 0.6
0.6
0.90
0.4
0.4
-0.5 0.85 -0.5 -0.5 0.2
-0.5 0 0.5 -0.5 0 0.5 -0.5 0 0.5
(a) 200 Hz MUSICካข (c) 600 Hz MUSICካข (e) 1000 Hz MUSICካข

0.5 0.5 0.5
0.8 0.8 0.8

0 0.6 0 0.6 0 0.6
0.4 0.4 0.4
0.2 0.2 0.2
-0.5 -0.5 -0.5
-0.5 0 0.5 -0.5 0 0.5 -0.5 0 0.5
(b) 200 Hzవ஡ካข (d) 600 Hzవ஡ካข (f) 1000 Hzవ஡ካข
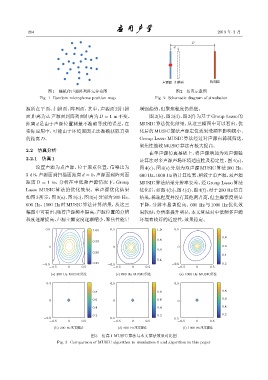
图 3 仿真 1 MUSIC 算法与本文算法效果对比图
Fig. 3 Comparison of MUSIC algorithm in simulation 1 and algorithm in this paper