Page 113 - 应用声学2019年第2期

第 38 卷 第 2 期 李均浩等： 一种改进的非整数自适应时延估计方法 259

比迭代步长为 0.19。在整个区间上，改进算法的较 中，LMPFTDE 算法估计误差较改进算法较大。表
低均方根误差在同一条折线上，曲线平稳，其时延收 明可以选取对应参数，使其在不同脉冲强度下均有
敛因子与信噪比迭代步长为 0.29；在 α = 1.2 到 1.6 较好的估计性能。

0.25
ͥᝠᄊکவಪ (sample) 0.15
0.20

0.10
0.05

0
1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
α
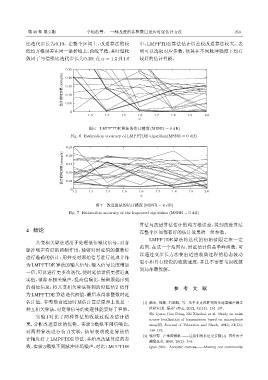
图 6 LMPFTDE 算法的估计精度 (MSNR = 0 dB)
Fig. 6 Estimation accuracy of LMPFTDE algorithm(MSNR = 0 dB)

0.25
ͥᝠᄊکவಪ (sample) 0.15
0.20

0.10

0.05
0
1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
α
图 7 改进算法的估计精度 (MSNR = 0 dB)
Fig. 7 Estimation accuracy of the improved algorithm (MSNR = 0 dB)

算法与改进算法估计的均方根误差，得到改进算法
4 结论 在整个区间都有好的估计效果的一组参数。

LMPFTDE 算法将迭代的初始值限定在一定
共变相关算法适用于处理低信噪比信号，对含
范围，在这一个范围内，时延估计值是单峰函数，可
脉冲噪声有好的抑制作用，能够对时延值的整数位
以通过变步长方法使自适应收敛过程的稳态波动
进行准确的估计；用共变对原始信号进行处理并作
更小和具有较快的收敛速度，并且不需要考虑收敛
为LMPFTDE算法的输入信号，输入信号长度增加
到局部最优解。
一倍，可以进行更多次迭代，使时延估计值更接近真
实值，消除不相关噪声，提高信噪比，保留原始序列
的相位信息；将共变相关算法得到的时延估计值作 参 考 文 献
为LMPFTDE算法迭代初值，最后求得非整数时延
估计值。非整数自适应时延估计算法原理上也是一 [1] 施全, 郭栋, 石晓辉, 等. 基于麦克风阵列的变速器噪声源定
种互相关算法，对宽带信号的处理性能要好于窄带。 位研究 [J]. 振动与冲击, 2012, 31(13): 134–137.
Shi Quan, Guo Dong, Shi Xiaohui, et al. Study on noise
实验 1 对比了两种算法的收敛过程及估计结
source localization of transmission based on microphone
果，分析改进算法的优势。实验 2 模拟不同信噪比， array[J]. Journal of Vibration and Shock, 2012, 31(13):
对两种算法进行仿真实验，结果表明改进算法估 134–137.
[2] 钱世锷. 声学照相机 ——让我们的社区更安静 [J]. 国外电子
计精度好于LMPFTDE算法，并给出改进算法的参
测量技术, 2009, 28(2): 5–8.
数。实验3模拟不同脉冲环境噪声，对比LMPFTDE Qian Shie. Acoustic camera——Making our community